搜索
【题目】温度的变化是人们在生活中经常谈论的话题，请你根据下图回答下列问题：
(1)上午9时的温度是多少？这一天的最高温度是多少？
(2)这一天的温差是多少？从最低温度到最高温度经过了多长时间？
(3)在什么时间范围内温度在下降？图中的A点表示的是什么？
参考答案：
【答案】(1)27℃，37℃；(2)14℃，12小时；(3)0时至3时及15时至24时， A点表示21点时的气温．
【解析】
(1)观察函数图象找出时间9时的温度和这一天的最高温度；
(2)找出函数图象的最高点（最高温度）和最低点（最低温度），然后再找最高点和最低点分别对应的时间；用最高温度减去最低温度得到这天的温差，最低温度到最高温度经过的时间等于最高点和最低点对应的时间的差；
(3)观察图象0时到3时和15时到24时温度在下降.
解：(1)利用图象得出上午9时的温度是27℃，这一天的最高温度是37℃.
(2)这一天的温差是37－23＝14(℃)，从最低温度到最高温度经过了15－3＝12(小时)．
(3)温度下降的时间范围为0时至3时及15时至24时，图中的A点表示的是21点时的气温．
故答案为：(1)27℃，37℃；(2)14℃，12小时；(3)0时至3时及15时至24时， A点表示21点时的气温．
-
科目： 来源： 题型：
查看答案和解析>>【题目】筹建中的城南中学需720套单人课桌椅（如图），光明厂承担了这项生产任务．该厂生产桌子必须5人一组．每组每天可生产12张；生产椅子必须4人一组，每组每天可生产24把．已知学校筹建组要求光明厂6天完成这项生产任务．
（1）问光明厂平均毎天要生产多少套单人课桌椅？
（2）现学校筹建组要求至少提前1天完成这项生产任务．光明厂生产课桌椅的员工增加到84名，试给出一种分配生产桌子、椅子的员工数的方案． -
科目： 来源： 题型：
查看答案和解析>>【题目】数学课上，李老师出示了如下框中的题目．
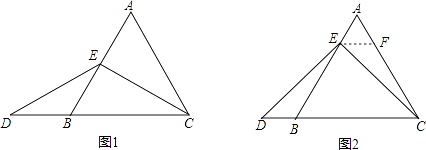
小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况探索结论
当点E为AB的中点时，如图1，确定线段AE与的DB大小关系．请你直接写出结论：AEDB（填“＞”，“＜”或“=”）．
（2）特例启发，解答题目
解：题目中，AE与DB的大小关系是：AEDB（填“＞”，“＜”或“=”）．理由如下：
如图2，过点E作EF∥BC，交AC于点F，（请你完成以下解答过程）
（3）拓展结论，设计新题
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长（请你直接写出结果）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，用长为20的铁丝焊接成一个长方形，设长方形的一边为x，面积为y，随着x的变化，y的值也随之变化．
(1)写出y与x之间的关系式，并指出在这个变化中，哪个是自变量？哪个是因变量？
(2)用表格表示当x从1变化到9时(每次增加1)，y的相应值；
x
1
2
3
4
5
6
7
8
9
y
(3)当x为何值时，y的值最大？
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两地相距210千米，一辆货车将货物由甲地运至乙地，卸载后返回甲地．若货车距乙地的距离y(千米)与时间t(时)的关系如图所示，根据所提供的信息，回答下列问题：
(1)货车在乙地卸货停留了多长时间？
(2)货车往返速度，哪个快？返回速度是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在如下三个函数图象中，有两个函数图象能近似地刻画如下
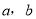两个情境：
情境
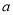：小芳离开家不久，发现把作业本忘在家里，于是返回家里找到了作业本再去学校；情境
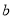：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进.（1）情境
， 
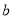所对应的函数图象分别为 ， （填写序号）．（2）请你为剩下的函数图象写出一个适合的情境．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=﹣
（x﹣1）2+3与y轴交于点A，顶点为B，对称轴BC与x轴交于点C．
（1）如图1．求点A的坐标及线段OC的长；
（2）点P在抛物线上，直线PQ∥BC交x轴于点Q，连接BQ．
①若含45°角的直角三角板如图2所示放置．其中，一个顶点与点C重合，直角顶点D在BQ上，另一个顶点E在PQ上．求直线BQ的函数解析式；
②若含30°角的直角三角板一个顶点与点C重合，直角顶点D在直线BQ上，另一个顶点E在PQ上，求点P的坐标．
相关试题
