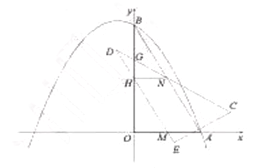
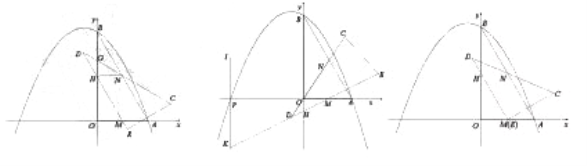
【题目】如图1,在平面直角坐标系中,![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.![]() ,且
,且![]() 始终保持边
始终保持边![]() 经过点
经过点![]() ,边
,边![]() 经过点
经过点![]() ,边
,边![]() 与
与![]() 轴交于点
轴交于点![]() ,边
,边![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)填空,![]() 的长是 ,
的长是 ,![]() 的度数是 度
的度数是 度
(2)如图2,当![]() ,连接
,连接![]()
①求证:四边形![]() 是平行四边形;
是平行四边形;
②判断点![]() 是否在抛物线的对称轴上,并说明理由;
是否在抛物线的对称轴上,并说明理由;
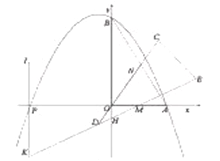
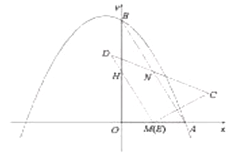
(3)如图3,当边![]() 经过点
经过点![]() 时(此时点
时(此时点![]() 与点
与点![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 延长线上于点
延长线上于点![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() (若
(若![]() 在直线
在直线![]() 的同侧),连接
的同侧),连接![]() ,请直接写出的
,请直接写出的![]() 长.
长.
参考答案:
【答案】(1)8,30;(2)①详见解析;②点D在该抛物线的对称轴上,理由详见解析;(3)12![]() .
.
【解析】
试题分析:(1)根据抛物线的解析式![]() 求得点A的坐标为(8,0),点B的坐标为(0,8
求得点A的坐标为(8,0),点B的坐标为(0,8![]() ),即可得OA=8,根据锐角三角函数的定义即可求得
),即可得OA=8,根据锐角三角函数的定义即可求得![]() =30°;(2)①由
=30°;(2)①由![]() ,根据平行线分线段成比例定理可得
,根据平行线分线段成比例定理可得![]() ,又因OM=AM,可得OH=BH,再由BN=AN,根据三角形的中位线定理可得
,又因OM=AM,可得OH=BH,再由BN=AN,根据三角形的中位线定理可得![]() ,即可判定四边形AMHN是平行四边形;②点D在该抛物线的对称轴上,如图,过点D作DR
,即可判定四边形AMHN是平行四边形;②点D在该抛物线的对称轴上,如图,过点D作DR![]() y轴于点R,由
y轴于点R,由![]() 可得∠NHB=∠AOB=90°,由
可得∠NHB=∠AOB=90°,由![]() ,可得∠DHB=∠OBA=30°,又因
,可得∠DHB=∠OBA=30°,又因![]() ,根据全等三角形的性质可得∠HDG=∠OBA=30°,即可得∠HDN=∠HND,所以DH=HN=
,根据全等三角形的性质可得∠HDG=∠OBA=30°,即可得∠HDN=∠HND,所以DH=HN=![]() OA=4,在Rt△DHR中,DR=
OA=4,在Rt△DHR中,DR=![]() DH=
DH=![]() ,即可判定点D的横坐标为-2.又因抛物线的对称轴为直线
,即可判定点D的横坐标为-2.又因抛物线的对称轴为直线![]() ,所以点D在该抛物线的对称轴上;
,所以点D在该抛物线的对称轴上;
试题解析:(1)8,30;
(2)①证明:∵![]() ,
,
∴![]() ,
,
又∵OM=AM,
∴OH=BH,
又∵BN=AN
∴![]()
∴四边形AMHN是平行四边形
②点D在该抛物线的对称轴上,理由如下:
如图,过点D作DR![]() y轴于点R,
y轴于点R,
∵![]()
∴∠NHB=∠AOB=90°,
∵![]() ,
,
∴∠DHB=∠OBA=30°,
又∵![]()
∴∠HDG=∠OBA=30°,
∴∠HDG=∠DHB=30°,
∴∠HGN=2∠HDG=60°,
∴∠HNG=90°-∠HGN=90°-60°=30°,
∴∠HDN=∠HND,
∴DH=HN=![]() OA=4
OA=4
在Rt△DHR中,DR=![]() DH=
DH=![]() ,
,
∴点D的横坐标为-2.
又因抛物线的对称轴为直线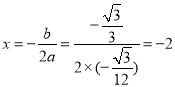 ,
,
∴点D在该抛物线的对称轴上.
(3)12![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他。随机调查了该校
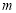 名学生(每名学生必须且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
名学生(每名学生必须且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图: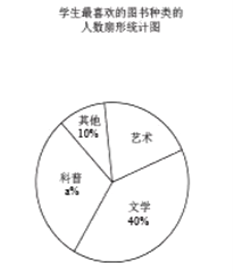
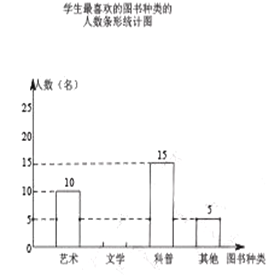
根据统计图提供的信息,解答下列问题:
(1)
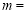 ,
,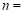 ;
;(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度.
(3)请根据以上信息直接在答题卡中补全条形统计图;
(4)根据抽样调查的结果,请你估计该校600名学生中有多少学生最喜欢科普类图书.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
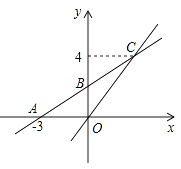
(1)求正比例函数与一次函数的关系式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
(4)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
 是边长为4的正方形,点
是边长为4的正方形,点 在边
在边 所在的直线上,连接
所在的直线上,连接 ,以
,以 为边,作正方形
为边,作正方形 (点
(点 ,点
,点 在直线
在直线 的同侧),连接
的同侧),连接
(1)如图1,当点
 与点
与点 重合时,请直接写出
重合时,请直接写出 的长;
的长;(2)如图2,当点
 在线段
在线段 上时,
上时,
①求点
 到
到 的距离
的距离②求
 的长
的长(3)若
 ,请直接写出此时
,请直接写出此时 的长.
的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 在
在 上,
上,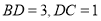 ,点
,点 是
是 上的动点,则
上的动点,则 的最小值为( )
的最小值为( )
A. 4 B.5 C. 6 D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】把命题“全等三角形的对应边相等”改写成“如果……,那么……”的形式:
____________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,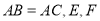 分别是
分别是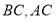 的中点,以
的中点,以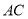 为斜边作
为斜边作 ,若
,若 ,则下列结论不正确的是( )
,则下列结论不正确的是( )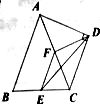
A.
 B.
B. 平分
平分 C.
C.  D.
D.
相关试题

