【题目】如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).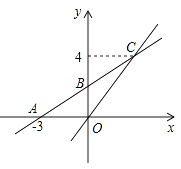
(1)求正比例函数与一次函数的关系式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
(4)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
参考答案:
【答案】
(1)解:∵一次函数y=k1x+b过点A(-3,0); C(3,4)
∴ ![]() 解得:
解得: 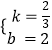
∴一次函数关系式为y= ![]() x+2
x+2
∵正比例函数y=kx的图象过点为C(3,4)
∴4=-3k2
∴k2= ![]() 正比例函数:y=
正比例函数:y= ![]() x
x
(2)解:如图所示,作D1M⊥X轴于M点,作D2N⊥Y轴于N,在等腰△AD1B中,
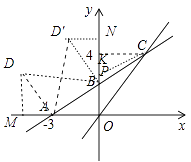
A D1=AB ; ∠D1AB=90° ∠D1DA=∠AOB=90°
∴∠D1AM+∠BAO=90° 又∵∠ABO+∠BAO=90°
∴∠D1AM =∠BAO
在△D1DA与△ OAB中
∠D1AM =∠BAO(已证)
∠D1MA=∠AOB(已证)
A D1=AB (已证)
∴△D1MA≌△OAB(AAS)
∴D1 M=OA=3;AM=BO=2 ∴OM=5
∵D1在第二象限,∴D1(-5,3)
同理证:△D2NB≌△BOA(AAS) ∴D2(-2,5)
(3)解:存在;作C关于X轴对称点C1,连接BC1,交X轴于E,此时△BCE周长最小。
∵ ![]() ∴
∴ ![]()
∴BC1的解析式为:y=-2x+2
令y=0,得0=-2x+2, x=1
∴E点的坐标为(1,0)
(4)解:P (5,0)
P (-5,0)
P (6, 0)
P ( ![]() ,0)
,0)
【解析】(4)①当OC是腰,O是顶角的顶点时,OP=OC,则点P的坐标为(5,0)或(-5,0);
②当OC是腰,C是顶角的顶点时,CP=CP,则点P与点O关于x=3对称,则点P的坐标为(6,0);
③当OC是底边时,设点P的坐标为(a,0),则(a-3)2+42=a2,解得a=![]() ,则点P的坐标为(
,则点P的坐标为(![]() ,0).
,0).
综上可知,点P的坐标(5,0)或(-5,0)或(6,0)或(![]() ,0).
,0).
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小,以及对一次函数的图象和性质的理解,了解一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区的电力资源丰富,并且得到了较好的开发。该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费. 月用电量x(度)与相应电费y(元)之间的函数图像如图所示.
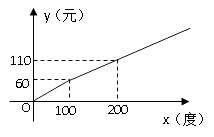
(1)月用电量为100度时,应交电费元;
(2)当x≥100时,求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他。随机调查了该校
 名学生(每名学生必须且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
名学生(每名学生必须且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图: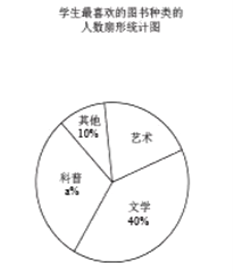
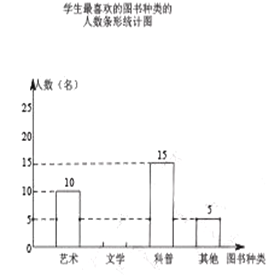
根据统计图提供的信息,解答下列问题:
(1)
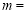 ,
, ;
;(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度.
(3)请根据以上信息直接在答题卡中补全条形统计图;
(4)根据抽样调查的结果,请你估计该校600名学生中有多少学生最喜欢科普类图书.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
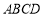 是边长为4的正方形,点
是边长为4的正方形,点 在边
在边 所在的直线上,连接
所在的直线上,连接 ,以
,以 为边,作正方形
为边,作正方形 (点
(点 ,点
,点 在直线
在直线 的同侧),连接
的同侧),连接
(1)如图1,当点
 与点
与点 重合时,请直接写出
重合时,请直接写出 的长;
的长;(2)如图2,当点
 在线段
在线段 上时,
上时,
①求点
 到
到 的距离
的距离②求
 的长
的长(3)若
 ,请直接写出此时
,请直接写出此时 的长.
的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
 是坐标原点,抛物线
是坐标原点,抛物线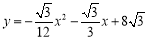 与
与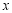 轴正半轴交于点
轴正半轴交于点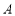 ,与
,与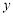 轴交于点
轴交于点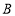 ,连接
,连接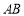 ,点
,点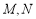 分别是
分别是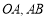 的中点.
的中点.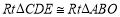 ,且
,且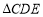 始终保持边
始终保持边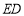 经过点
经过点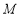 ,边
,边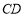 经过点
经过点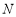 ,边
,边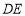 与
与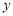 轴交于点
轴交于点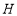 ,边
,边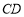 与
与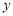 轴交于点
轴交于点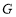 .
.(1)填空,
 的长是 ,
的长是 ,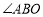 的度数是 度
的度数是 度(2)如图2,当
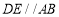 ,连接
,连接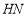
①求证:四边形
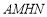 是平行四边形;
是平行四边形;②判断点
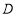 是否在抛物线的对称轴上,并说明理由;
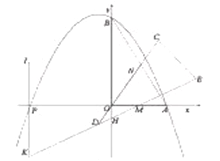
是否在抛物线的对称轴上,并说明理由;(3)如图3,当边
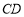 经过点
经过点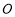 时(此时点
时(此时点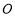 与点
与点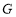 重合),过点
重合),过点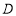 作
作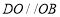 ,交
,交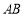 延长线上于点
延长线上于点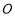 ,延长
,延长 到点
到点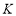 ,使
,使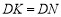 ,过点
,过点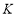 作
作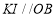 ,在
,在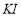 上取一点
上取一点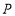 ,使得
,使得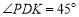 (若
(若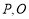 在直线
在直线 的同侧),连接
的同侧),连接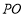 ,请直接写出的
,请直接写出的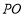 长.
长.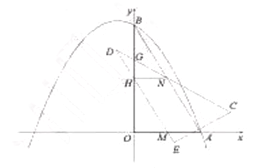
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 在
在 上,
上,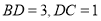 ,点
,点 是
是 上的动点,则
上的动点,则 的最小值为( )
的最小值为( )
A. 4 B.5 C. 6 D.7
相关试题

