【题目】四边形![]() 是边长为4的正方形,点
是边长为4的正方形,点![]() 在边
在边![]() 所在的直线上,连接
所在的直线上,连接![]() ,以
,以![]() 为边,作正方形
为边,作正方形![]() (点
(点![]() ,点
,点![]() 在直线
在直线![]() 的同侧),连接
的同侧),连接![]()
(1)如图1,当点![]() 与点
与点![]() 重合时,请直接写出
重合时,请直接写出![]() 的长;
的长;
(2)如图2,当点![]() 在线段
在线段![]() 上时,
上时,![]()
①求点![]() 到
到![]() 的距离
的距离
②求![]() 的长
的长
(3)若![]() ,请直接写出此时
,请直接写出此时![]() 的长.
的长.



参考答案:
【答案】(1)BF=4![]() ;(2)①点
;(2)①点![]() 到
到![]() 的距离为3;②BF=
的距离为3;②BF=![]() ;(3)AE=2+
;(3)AE=2+![]() 或AE=1.
或AE=1.
【解析】
试题分析:(1)过点F作FM![]() BA, 交BA的延长线于点M,根据勾股定理求得AC=
BA, 交BA的延长线于点M,根据勾股定理求得AC=![]() ,又因点
,又因点![]() 与点
与点![]() 重合,可得△AFM为等腰直角三角形且AF=
重合,可得△AFM为等腰直角三角形且AF=![]() ,再由勾股定理求得AM=FM=4,在Rt△BFM中,由勾股定理即可求得BF=4
,再由勾股定理求得AM=FM=4,在Rt△BFM中,由勾股定理即可求得BF=4![]() ;(2)①过点F作FH
;(2)①过点F作FH![]() AD交AD的延长线于点H,根据已知条件易证
AD交AD的延长线于点H,根据已知条件易证![]() ,根据全等三角形的性质可得FH=ED,又因AD=4,AE=1,所以ED=AD-AE=4-1=3,即可求得FH=3,即点
,根据全等三角形的性质可得FH=ED,又因AD=4,AE=1,所以ED=AD-AE=4-1=3,即可求得FH=3,即点![]() 到
到![]() 的距离为3;②延长FH交BC的延长线于点K,求得FK和BK的长,在Rt△BFK中,根据勾股定理即可求得BF的长;(3)分点E在线段AD的延长线上和点E在线段DA的延长线上两种情况求解即可.
的距离为3;②延长FH交BC的延长线于点K,求得FK和BK的长,在Rt△BFK中,根据勾股定理即可求得BF的长;(3)分点E在线段AD的延长线上和点E在线段DA的延长线上两种情况求解即可.
试题解析:
(1)BF=4![]() ;
;
(2) 如图,
①过点F作FH![]() AD交AD的延长线于点H,
AD交AD的延长线于点H,
∵四边形CEFG是正方形
∴EC=EF,∠FEC=90°
∴∠DEC+∠FEH=90°,
又因四边形![]() 是正方形
是正方形
∴∠ADC=90°
∴∠DEC+∠ECD=90°,
∴∠ECD=∠FEH
又∵∠EDC=∠FHE=90°,
∴![]()
∴FH=ED
∵AD=4,AE=1,
∴ED=AD-AE=4-1=3,
∴FH=3,
即点![]() 到
到![]() 的距离为3.
的距离为3.
②延长FH交BC的延长线于点K,
∴∠DHK=∠HDC=∠DCK =90°,
∴四边形CDHK为矩形,
∴HK=CD=4,
∴FK=FH+HK=3+4=7
∵![]()
∴EH=CD=AD=4
∴AE=DH=CK=1
∴BK=BC+CK=4+1=5,
在Rt△BFK中,BF=![]()

(3)AE=2+![]() 或AE=1.
或AE=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他。随机调查了该校
 名学生(每名学生必须且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
名学生(每名学生必须且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图: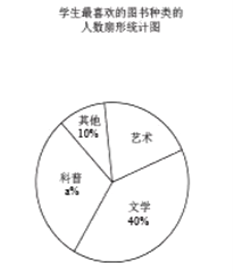
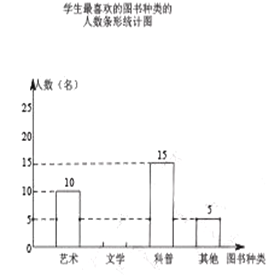
根据统计图提供的信息,解答下列问题:
(1)
 ,
, ;
;(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度.
(3)请根据以上信息直接在答题卡中补全条形统计图;
(4)根据抽样调查的结果,请你估计该校600名学生中有多少学生最喜欢科普类图书.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
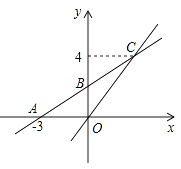
(1)求正比例函数与一次函数的关系式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
(4)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
 是坐标原点,抛物线
是坐标原点,抛物线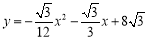 与
与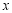 轴正半轴交于点
轴正半轴交于点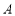 ,与
,与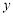 轴交于点
轴交于点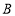 ,连接
,连接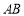 ,点
,点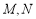 分别是
分别是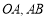 的中点.
的中点.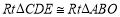 ,且
,且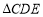 始终保持边
始终保持边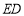 经过点
经过点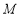 ,边
,边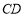 经过点
经过点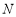 ,边
,边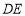 与
与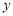 轴交于点
轴交于点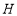 ,边
,边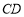 与
与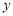 轴交于点
轴交于点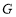 .
.(1)填空,
 的长是 ,
的长是 ,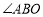 的度数是 度
的度数是 度(2)如图2,当
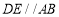 ,连接
,连接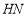
①求证:四边形
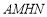 是平行四边形;
是平行四边形;②判断点
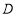 是否在抛物线的对称轴上,并说明理由;
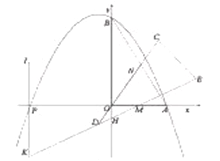
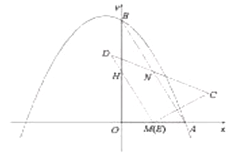
是否在抛物线的对称轴上,并说明理由;(3)如图3,当边
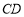 经过点
经过点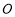 时(此时点
时(此时点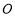 与点
与点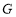 重合),过点
重合),过点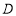 作
作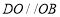 ,交
,交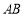 延长线上于点
延长线上于点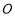 ,延长
,延长 到点
到点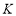 ,使
,使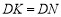 ,过点
,过点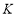 作
作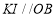 ,在
,在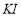 上取一点
上取一点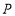 ,使得
,使得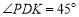 (若
(若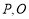 在直线
在直线 的同侧),连接
的同侧),连接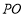 ,请直接写出的
,请直接写出的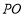 长.
长.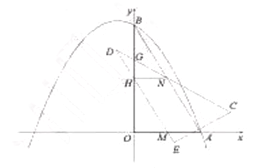
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 在
在 上,
上,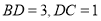 ,点
,点 是
是 上的动点,则
上的动点,则 的最小值为( )
的最小值为( )
A. 4 B.5 C. 6 D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】把命题“全等三角形的对应边相等”改写成“如果……,那么……”的形式:
____________________________
相关试题

