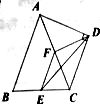
【题目】如图,在![]() 中,
中,![]() 分别是
分别是![]() 的中点,以
的中点,以![]() 为斜边作
为斜边作![]() ,若
,若![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A. ![]() B.
B.![]() 平分
平分![]() C.
C. ![]() D.
D.![]()
参考答案:
【答案】C.
【解析】
试题分析:由AB=AC,∠CAB=45°,根据等边对等角及三角形内角和定理求出∠B=∠ACB=67.5°.由Rt△ADC中,∠CAD=45°,∠ADC=90°,根据三角形内角和定理求出∠ACD=45°,根据等角对等边得出AD=DC,那么∠ECD=∠ACB+∠ACD=112.5°,从而判断A正确;根据三角形的中位线定理得到FE=![]() AB,FE∥AB,根据平行线的性质得出∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.根据直角三角形的性质以及等腰三角形的性质得到FD=
AB,FE∥AB,根据平行线的性质得出∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.根据直角三角形的性质以及等腰三角形的性质得到FD=![]() AC,DF⊥AC,∠FDC=45°,等量代换得到FE=FD,再求出∠FDE=∠FED=22.5°,进而判断B正确;
AC,DF⊥AC,∠FDC=45°,等量代换得到FE=FD,再求出∠FDE=∠FED=22.5°,进而判断B正确;
由∠FEC=∠B=67.5°,∠FED=22.5°,求出∠DEC=∠FEC﹣∠FED=45°,从而判断C错误;
在等腰Rt△ADC中利用勾股定理求出AC=![]() CD,又AB=AC,等量代换得到AB=
CD,又AB=AC,等量代换得到AB=![]() CD,从而判断D正确.
CD,从而判断D正确.
∵AB=AC,∠CAB=45°,∴∠B=∠ACB=67.5°.
∵Rt△ADC中,∠CAD=45°,∠ADC=90°,∴∠ACD=45°,AD=DC,
∴∠ECD=∠ACB+∠ACD=112.5°,故A正确,不符合题意;
∵E、F分别是BC、AC的中点,∴FE=![]() AB,FE∥AB,
AB,FE∥AB,
∴∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.
∵F是AC的中点,∠ADC=90°,AD=DC,∴FD=![]() AC,DF⊥AC,∠FDC=45°,
AC,DF⊥AC,∠FDC=45°,
∵AB=AC,∴FE=FD,
∴∠FDE=∠FED=![]() (180°﹣∠EFD)=
(180°﹣∠EFD)=![]() (180°﹣135°)=22.5°,
(180°﹣135°)=22.5°,
∴∠FDE=![]() ∠FDC,∴DE平分∠FDC,故B正确,不符合题意;
∠FDC,∴DE平分∠FDC,故B正确,不符合题意;
∵∠FEC=∠B=67.5°,∠FED=22.5°,
∴∠DEC=∠FEC﹣∠FED=45°,故C错误,符合题意;
∵Rt△ADC中,∠ADC=90°,AD=DC,
∴AC=![]() CD,∵AB=AC,
CD,∵AB=AC,
∴AB=![]() CD,故D正确,不符合题意.
CD,故D正确,不符合题意.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
 是坐标原点,抛物线
是坐标原点,抛物线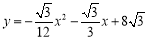 与
与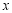 轴正半轴交于点
轴正半轴交于点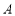 ,与
,与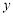 轴交于点
轴交于点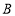 ,连接
,连接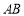 ,点
,点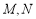 分别是
分别是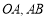 的中点.
的中点.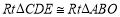 ,且
,且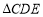 始终保持边
始终保持边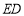 经过点
经过点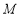 ,边
,边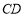 经过点
经过点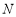 ,边
,边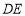 与
与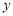 轴交于点
轴交于点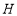 ,边
,边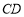 与
与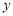 轴交于点
轴交于点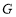 .
.(1)填空,
 的长是 ,
的长是 ,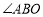 的度数是 度
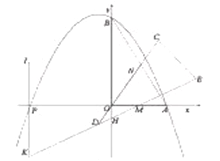
的度数是 度(2)如图2,当
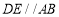 ,连接
,连接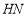
①求证:四边形
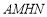 是平行四边形;
是平行四边形;②判断点
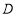 是否在抛物线的对称轴上,并说明理由;
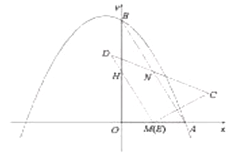
是否在抛物线的对称轴上,并说明理由;(3)如图3,当边
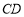 经过点
经过点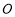 时(此时点
时(此时点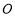 与点
与点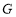 重合),过点
重合),过点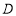 作
作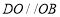 ,交
,交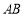 延长线上于点
延长线上于点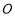 ,延长
,延长 到点
到点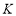 ,使
,使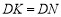 ,过点
,过点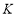 作
作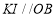 ,在
,在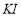 上取一点
上取一点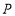 ,使得
,使得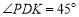 (若
(若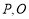 在直线
在直线 的同侧),连接
的同侧),连接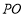 ,请直接写出的
,请直接写出的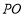 长.
长.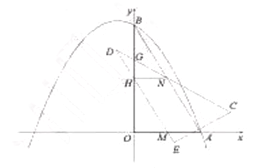
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 在
在 上,
上,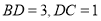 ,点
,点 是
是 上的动点,则
上的动点,则 的最小值为( )
的最小值为( )
A. 4 B.5 C. 6 D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】把命题“全等三角形的对应边相等”改写成“如果……,那么……”的形式:
____________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为(用n表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
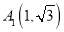 在直线
在直线 上,过点
上,过点 作
作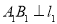 交直线
交直线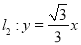 于点
于点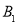 ,
, 为边在
为边在 外侧作等边三角形
外侧作等边三角形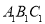 ,再过点
,再过点 作
作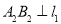 ,分别交直线
,分别交直线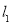 和
和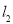 于
于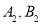 两点,以
两点,以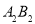 为边在
为边在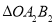 外侧作等边三角形
外侧作等边三角形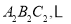 按此规律进行下去,则第
按此规律进行下去,则第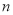 个等边三角形
个等边三角形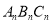 的面积为__________.(用含
的面积为__________.(用含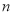 的代数式表示)
的代数式表示)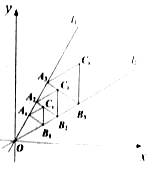
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2+a2=a4
B.a6÷a2=a4
C.(a2)3=a5
D.(a﹣b)2=a2﹣b2
相关试题

