【题目】(1)如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长.
(2)一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
参考答案:
【答案】(1)![]() (2)22
(2)22
【解析】
(1)由平移的性质可知BE=2BC=4,DE=AC=2,故可得出BD⊥DE,由∠E=∠ACB=60°可知AC∥DE,根据勾股定理即可得出BD的长.
(2)将答对题数所得的分数减去打错或不答所扣的分数,在由题意知小明答题所得的分数大于等于85分,列出不等式即可.
(1)解:∵正△ABC沿直线BC向右平移得到正△DCE,
∴ BE=2BC=4, BC=CD,DE=AC=2,∠E=∠ACB=∠DCE=∠ABC=60°,
∴∠DBE=![]() ∠DCE =30°,
∠DCE =30°,
∴∠BDE=90°,
在Rt△BDE中,由勾股定理得,
![]()
(2)解:设小明答对了x道题,
4x-(25-x) ≥85,
x≥22,
所以,小明至少答对了22道题.
-
科目: 来源: 题型:
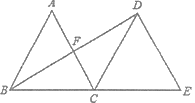
查看答案和解析>>【题目】如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
-
科目: 来源: 题型:
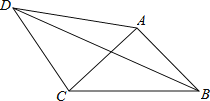
查看答案和解析>>【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
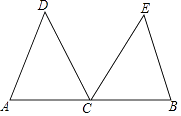
(1)求证:△ACD≌△BCE;
(2)若∠D=53°,求∠B的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+3的图象与反比例y=
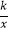 (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.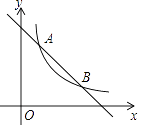
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=
 ,BE=
,BE= .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC是弦,过点O作OE⊥BC于H交⊙O于E,在OE的延长线上取一点D,使∠ODB=∠AEC,AE与BC交于F.
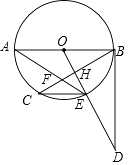
(1)判断直线BD与⊙O的位置关系,并给出证明;
(2)当⊙O的半径是5,BF=2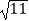 ,EF=
,EF= 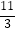 时,求CE及BH的长.
时,求CE及BH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣bx+c过点B(3,0),C(0,﹣3),D为抛物线的顶点.
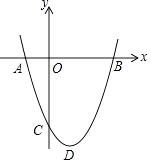
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点,连接BC,BE,求∠CBE的正切值;
(3)在(2)的条件下,点M是抛物线对称轴上且在CE上方的一点,是否存在点M使△DMB和△BCE相似?若存在,求点M坐标;若不存在,请说明理由.
相关试题

