【题目】如图,抛物线y=x2﹣bx+c过点B(3,0),C(0,﹣3),D为抛物线的顶点.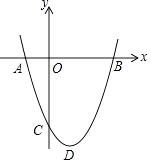
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点,连接BC,BE,求∠CBE的正切值;
(3)在(2)的条件下,点M是抛物线对称轴上且在CE上方的一点,是否存在点M使△DMB和△BCE相似?若存在,求点M坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:设抛物线的解析式为y=(x+3)(x+n),将点C的坐标代入得:3n=﹣3,解得n=﹣1.
∴抛物线的解析式为y=(x+3)(x﹣1)即y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4)
(2)
解:如图1所示:过点E作ED⊥BC,垂足为D.
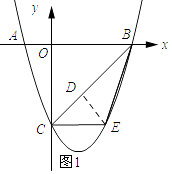
∵B(3,0),C(0,﹣3),
∴OC=OB=3.
∴∠OCB=∠OBC=45°,BC=3 ![]()
∵点E与点C关于抛物线的对称轴对称,
∴CE⊥OC,
∴∠DCE=45°.
∵ED⊥CD,
∴△DEB为等腰直角三角形.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴为x=1.
∴CE=2.
∴CD=ED= ![]() .
.
∴BD=BC﹣CD=2 ![]() .
.
∴tan∠CBE= ![]() =
= ![]()
(3)
解:如图2所示:
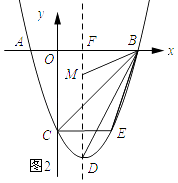
∵B(3,0),D(﹣1,﹣4),
∴A(﹣1,0),F(1,0).
∴FB=2,DF=4.
∴tan∠FDB= ![]() .
.
∴tan∠FDB=tan∠CBE.
∴∠FDB=∠CBE.
∴当 ![]() =
= ![]() 时,△BCE∽△DBM.
时,△BCE∽△DBM.
∴ ![]() =
= ![]() ,解得:MD=
,解得:MD= ![]() .
.
∴点M的纵坐标=﹣4+ ![]() =﹣
=﹣ ![]() .
.
∴M(1,﹣ ![]() ).
).
如图3所示:
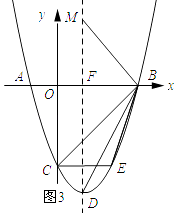
∵∠FDB=∠CBE,
∴当∠BMD=∠BCE=45°时,△DMB∽△BCE.
∴FM=FB=2.
∴M(1,2).
综上所述,当点M的坐标为(1,﹣ ![]() )或(1,2)时,△DMB和△BCE相似
)或(1,2)时,△DMB和△BCE相似
【解析】(1)设抛物线的解析式为y=(x+3)(x+n),将点C的坐标代入可求得n的值,则可得到抛物线的解析式,然后利用配方法可求得抛物线的顶点坐标;(2)过点E作ED⊥BC,垂足为D.由题意可得到△OBC和△CDE均为等腰直角三角形,然后求得CE、BC、DE的长,最后利用锐角三角函数的定义求解即可;(3)先证明tan∠FDB=tan∠CBE,从而得到∠FDB=∠CBE,当 ![]() =
= ![]() 或当∠BMD=∠BCE=45°时,△DMB和△BCE相似.
或当∠BMD=∠BCE=45°时,△DMB和△BCE相似.
-
科目: 来源: 题型:
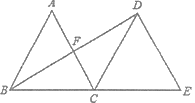
查看答案和解析>>【题目】(1)如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长.
(2)一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,∠DCE=30°,DE=
 ,BE=
,BE= .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC是弦,过点O作OE⊥BC于H交⊙O于E,在OE的延长线上取一点D,使∠ODB=∠AEC,AE与BC交于F.
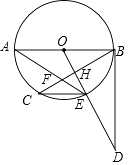
(1)判断直线BD与⊙O的位置关系,并给出证明;
(2)当⊙O的半径是5,BF=2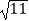 ,EF=
,EF= 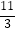 时,求CE及BH的长.
时,求CE及BH的长. -
科目: 来源: 题型:
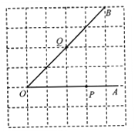
查看答案和解析>>【题目】如图,点P,Q分别是∠AOB的边OA,OB上的点.
(1)过点P画OB的垂线,垂足为H;
(2)过点Q画OA的垂线,交OA于点C,连接PQ;
(3)线段QC的长度是点Q到 的距离, 的长度是点P到直线OB的距离,因为直线外一点和直线上各点连接的所有线段中,垂线段最短,所以线段PQ、PH的大小关系是 (用“<”号连接).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
(1)如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是 ;
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料.
点M,N在数轴上分别表示数m和n,我们把m,n之差的绝对值叫做点M,N之间的距离,即MN=|m﹣n|.如图,在数轴上,点A,B,O,C,D的位置如图所示,则DC=|3﹣1|=|2|=2;CO=|1﹣0|=|1|=1;BC=|(﹣2)﹣1|=|﹣3|=3;AB=|(﹣4)﹣(﹣2)|=|﹣2|=2.

(1)OA= ,BD= ;
(2)|1﹣(﹣4)|表示哪两点的距离?
(3)点P为数轴上一点,其表示的数为x,用含有x的式子表示BP= ,当BP=4时,x= ;当|x﹣3|+|x+2|的值最小时,x的取值范围是 .
相关试题

