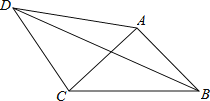
【题目】如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
参考答案:
【答案】![]() .
.
【解析】
试题根据等式的性质,可得∠BAD与∠CAD′的关系,根据SAS,可得△BAD与△CAD′的关系,根据全等三角形的性质,可得BD与CD′的关系,根据勾股定理,可得答案:
如答图,作AD′⊥AD,AD′=AD,连接CD′,DD′,
∵∠ABC=∠ACB=45°,∴BA=BC.
∵∠BAC+∠CAD=∠DAD′+∠CAD,即∠BAD=∠CAD′,
在△BAD与△CAD′中,∵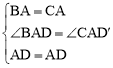 ,∴△BAD≌△CAD′(SAS).∴BD=CD′.
,∴△BAD≌△CAD′(SAS).∴BD=CD′.
在Rt△ADD′中,由勾股定理得![]() .
.
∵∠D′DA=∠ADC=45°,∴∠D′DC=90°.
在Rt△CDD′中,由勾股定理得![]() ,
,
∴BD=CD′=![]() .
.
-
科目: 来源: 题型:
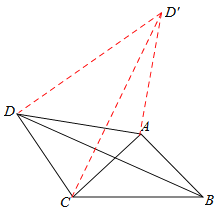
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,过点O作两条射线OM,ON,且∠AOM=∠CON=90°.
(1)若OC平分∠AOM,求∠AOD的度数;
(2)若∠1=∠BOC,求∠AOC和∠MOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

-
科目: 来源: 题型:
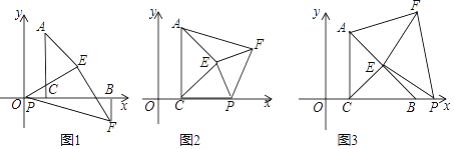
查看答案和解析>>【题目】如图,在△ABC中,点B,C是x轴上的两个定点,∠ACB=90°,AC=BC,点A(l,3),点P是x轴上的一个动点,点E是AB的中点,在△PEF中,∠PEF=90°,PE=EF
(1)如图1,当点P与坐标原点重合时:①求证△PCE≌△FBE;②求点F的坐标;
(2)如图2,当点P在线段CB上时,求证S△CPE=S△AEF
(3)如图3,当点P在线段CB的延长线时,若S△AEF=4S△PBE则此刻点F的坐标为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
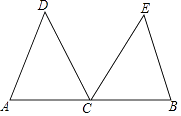
(1)求证:△ACD≌△BCE;
(2)若∠D=53°,求∠B的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+3的图象与反比例y=
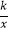 (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.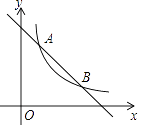
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长.
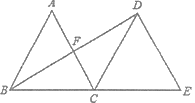
(2)一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
相关试题

