搜索
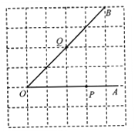
【题目】如图，在四边形ABCD中，对角线AC，BD交于点E，∠BAC=90°，∠CED=45°，∠DCE=30°，DE=
，BE=
．求CD的长和四边形ABCD的面积．
参考答案：
【答案】解：如图，过点D作DH⊥AC，
∵∠CED=45°，DH⊥EC，DE=
，∴EH=DH。
∵EH2+DH2=ED2，∴EH2=1。∴EH=DH=1。
又∵∠DCE=30°，∴CD=2，HC=
。
∵∠AEB=45°，∠BAC=90°，BE=
。∴AB=AE=2。
∴AC=2+1+
=3+
。
∴S四边形ABCD=
×2×（3+
）+
×1×（3+
）=
。
【解析】利用等腰直角三角形的性质得出EH=DH=1，进而得出再利用直角三角形中30°所对边等于斜边的一半得
出CD的长，求出AC，AB的长即可得出四边形ABCD的面积。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C是线段AB的中点，CD平分∠ACE，CE平分∠BCD，CD=CE．
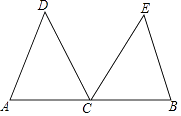
（1）求证：△ACD≌△BCE；
（2）若∠D=53°，求∠B的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=﹣x+3的图象与反比例y=
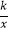（k为常数，且k≠0）的图象交于A（1，a），B两点．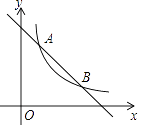
（1）求反比例函数的表达式及点B的坐标；
（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】(1)如图，△ABC是边长为2的等边三角形，将△ABC沿直线BC向右平移，使点B与点C重合，得到△DCE，连接BD，交AC于点F．求线段BD的长．
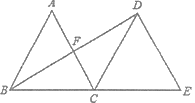
(2)一次环保知识竞赛共有25道题，规定答对一道题得4分，答错或不答一道题扣1分.在这次竞赛中，小明被评为优秀（85分或85分以上），小明至少答对了几道题？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，BC是弦，过点O作OE⊥BC于H交⊙O于E，在OE的延长线上取一点D，使∠ODB=∠AEC，AE与BC交于F．
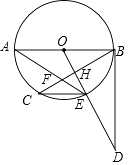
（1）判断直线BD与⊙O的位置关系，并给出证明；
（2）当⊙O的半径是5，BF=2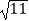
，EF=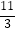 
时，求CE及BH的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=x2﹣bx+c过点B（3，0），C（0，﹣3），D为抛物线的顶点．
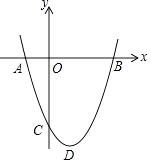
（1）求抛物线的解析式以及顶点坐标；
（2）点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点，连接BC，BE，求∠CBE的正切值；
（3）在（2）的条件下，点M是抛物线对称轴上且在CE上方的一点，是否存在点M使△DMB和△BCE相似？若存在，求点M坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P，Q分别是∠AOB的边OA，OB上的点.
(1)过点P画OB的垂线，垂足为H；
(2)过点Q画OA的垂线，交OA于点C，连接PQ；
(3)线段QC的长度是点Q到 的距离， 的长度是点P到直线OB的距离，因为直线外一点和直线上各点连接的所有线段中，垂线段最短，所以线段PQ、PH的大小关系是 (用“＜”号连接).
相关试题
