搜索
【题目】已知A、B、C、D是平面坐标系中坐标轴上的点，且△AOB≌△COD．设直线AB的表达式为y1=k1x+b1 ， 直线CD的表达式为y2=k2x+b2 ， 则k1k2= ． 
参考答案：
【答案】1
【解析】解：设点A（0，a）、B（b，0），
∴OA=a，OB=﹣b，
∵△AOB≌△COD，
∴OC=a，OD=﹣b，
∴C（a，0），D（0，b），
∴k1= 
= 
，k2= 
= 
，
∴k1k2=1，
故答案为：1．
根据A（0，a）、B（b，0），得到OA=a，OB=﹣b，根据全等三角形的性质得到OC=a，OD=﹣b，得到C（a，0），D（0，b），求得k1= ，k2= ，即可得到结论．本题考查了两直线相交与平行，全等三角形的性质，熟练掌握全等三角形的性质是解题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形内，在对角线AC上找到一点P，使PD+PE的和最小，则这个和的最小值是（ ）．
A.
B.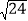 
C. 3 D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】长春外国语学校为了创建全省“最美书屋”，购买了一批图书，其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元.已知学校用12000元购买的科普类图书的本数与用9000元购买的文学类图书的本数相等，求学校购买的科普类图书和文学类图书平均每本的价格各是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC的内切圆的三个切点分别为D、E、F，∠A=75°，∠B=45°，则圆心角∠EOF=度．
-
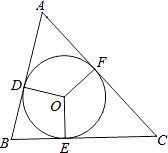
科目： 来源： 题型：
查看答案和解析>>【题目】为调查市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭轿车,E:其他”五个选项中选择最常用的一项，将所有调查结果整理后绘制成不完整的条形统计图（图1）和扇形统计图（图2），请结合统计图回答下列问题：
（1）在这次调查中，一共调查了 名市民；
（2）扇形统计图中，C组的百分率是 ；并补全条形统计图；
（3）计算四市中10000名市民上班时最常用家庭轿车的有多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，Rt△ABC中，∠C=90°，BC=6，AC=8.动点P从点A出发沿A—B—C的方向以每秒2个单位的速度运动.设P的运动时间为t（秒）.
（1）请直接用含t的代数式表示①当点P在AB上时，BP= ；②当点P在BC上时，BP= ；
（2）求△BPC为等腰三角形的t值.
(备用图) -
科目： 来源： 题型：
查看答案和解析>>【题目】定义，我们把对角线互相垂直的四边形叫做垂美四边形．
概念理解：如图②，在四边形ABCD中，如果AB=AD，CB=CD，那么四边形ABCD是垂美四边形吗？请说明理由．
性质探究：如图①，垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系？写出你的猜想，并给出证明．
问题解决：如图③，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连结CE、BG、GE．若AC=2，AB=5，则①求证：△AGB≌△ACE；
②GE= ．
相关试题
