【题目】小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
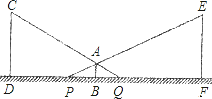
(1)小明距离路灯多远?
(2)求路灯高度.
参考答案:
【答案】(1)小明距离路灯12m;(2)路灯高6m.
【解析】试题分析:(1)易得△QAB∽△QCD,那么可得![]() ,同理可得
,同理可得![]() ,根据CD=EF,可得一个比例式,把相关数值代入可得所求数值;
,根据CD=EF,可得一个比例式,把相关数值代入可得所求数值;
(2)根据(1)得到的比例式及数值,计算可得路灯高度.
试题解析:(1)设DB=xm,
∵AB∥CD ,
∴∠QBA=∠QDC , ∠QAB=∠QCD ,
∴△QAB∽△QCD
∴![]()
同理可得![]()
∵CD=EF
∴![]()
∴![]()
∴x=12
即小明距离路灯12m .
(2)由 ![]() 得
得 ![]()
∴CD=6
即路灯高6m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家预测一种应季衬衫能畅销市场,就用13 200元购进了一批这种衬衫,面市后果然供不应求,商家又用28 800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完利润率不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并完成填空.
你能比较20152 016和20162 015的大小吗?
为了解决这个问题,先把问题一般化,比较nn+1和(n+1)n(n≥1,且n为整数)的大小.然后从分析n=1,n=2,n=3…的简单情形入手,从中发现规律,经过归纳、猜想得出结论.
(1)通过计算(可用计算器)比较下列①~⑦组两数的大小:(在横线上填上“>”“=”或“<”)
①12____21;②23_____32;③34_____43;④45_____54;
⑤56____65;⑥67_____76;⑦78_____87;
(2)归纳第(1)问的结果,可以猜想出nn+1和(n+1)n的大小关系;
(3)根据以上结论,可以得出20162017和20172016的大小关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内,正方形ABCD与正方形CEFH如图放置,连接DE,BH,两线交于M,求证:

(1)BH=DE;
(2)BH⊥DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
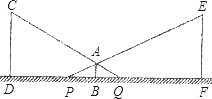
(1)小明距离路灯多远?
(2)求路灯高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
解答“已知
 ,且
,且 ,
, ,确定
,确定 的取值范围”有如下解,
的取值范围”有如下解,解:∵
 ,
,∴
 .
.又∵
 ,
,∴
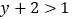 .
.∴
 .
.又∵
 ,
,∴
 ,
, ①
①同理得:
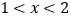 .
. ②
②由①
 ②得
②得 .
.∴
 的取值范围是
的取值范围是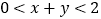 .
.请按照上述方法,完成下列问题:
(
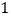 )已知
)已知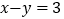 ,且
,且 ,
, ,求
,求 的取值范围.
的取值范围.(
 )已知
)已知 ,
, ,若
,若 ,且
,且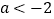 ,求
,求 得取值范围(结果用含
得取值范围(结果用含 的式子表示).
的式子表示). -
科目: 来源: 题型:
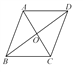
查看答案和解析>>【题目】已知如图所示,△AOB与△COD关于点O成中心对称,连接BC,AD.
(1)求证:四边形ABCD为平行四边形;
(2)若△AOB的面积为15 cm2,求四边形ABCD的面积.
相关试题

