【题目】阅读下列材料:
解答“已知![]() ,且
,且![]() ,
,![]() ,确定
,确定![]() 的取值范围”有如下解,
的取值范围”有如下解,
解:∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,![]() ①
①
同理得:![]() .
.![]() ②
②
由①![]() ②得
②得![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.
请按照上述方法,完成下列问题:
(![]() )已知
)已知![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
(![]() )已知
)已知![]() ,
,![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 得取值范围(结果用含
得取值范围(结果用含![]() 的式子表示).
的式子表示).
参考答案:
【答案】(1) 1<x+y<5;(2) a+2<x+y<-a-2.
【解析】整体分析:
(1)先分别确定x,y的取值范围,再根据等式的性质确定x+y的范围;(2)先分别用含a的式子确定x,y的取值范围,再根据等式的性质用含a的式子确定x+y的范围;
解:(1)∵x-y=3,∴x=y+3.
∵x>2,∴y+3>2,∴y>-1.
∵y<1,∴-1<y<1.…①
同理得:2<x<4.…②
由①+②得-1+2<y+x<1+4,
∴x+y的取值范围是1<x+y<5.
(2)∵x-y=a,∴x=y+a.
∵x<-1,∴y+a<-1,∴y<-a-1.
∵y>1,∴1<y<-a-1.…①
同理得:a+1<x<-1.…②
由①+②得1+a+1<y+x<-a-1+(-1),
∴x+y的取值范围是a+2<x+y<-a-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内,正方形ABCD与正方形CEFH如图放置,连接DE,BH,两线交于M,求证:

(1)BH=DE;
(2)BH⊥DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
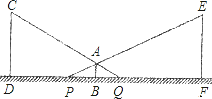
(1)小明距离路灯多远?
(2)求路灯高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
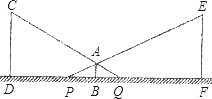
(1)小明距离路灯多远?
(2)求路灯高度.
-
科目: 来源: 题型:
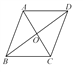
查看答案和解析>>【题目】已知如图所示,△AOB与△COD关于点O成中心对称,连接BC,AD.
(1)求证:四边形ABCD为平行四边形;
(2)若△AOB的面积为15 cm2,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接河北省中小学生健康体质测试,某学校开展“健康校园,阳光跳绳”活动,为此学校准备购置A,B,C三种跳绳.已知某厂家的跳绳的规格与价格如下表:
,A绳子,B绳子,C绳子长度(米),8,6,4单价(元/条),12,8,6
(1)已知购买A,B两种绳子共20条花了180元,问A,B两种绳子各购买了多少条?
(2)若该厂家有一根长200米的绳子,现将其裁成A,C两种绳子销售总价为240元,则剩余的绳子长度最多可加工几条B种绳子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

相关试题

