【题目】从﹣4、- ![]() 、0、
、0、 ![]() 、4这五个数中,任取一个数作为a的值,恰好使得关于x的一元二次方程2ax2﹣6x﹣1=0有两个不相等的实数根,且使两个根都在﹣1和1之间(包括﹣1和1),则取到满足条件的a值的概率为 .
、4这五个数中,任取一个数作为a的值,恰好使得关于x的一元二次方程2ax2﹣6x﹣1=0有两个不相等的实数根,且使两个根都在﹣1和1之间(包括﹣1和1),则取到满足条件的a值的概率为 .
参考答案:
【答案】![]()
【解析】解:∵当a=﹣4时,原方程可化为﹣8x2﹣6x﹣1=0,解得x1=﹣ ![]() ,x2=﹣
,x2=﹣ ![]() ,符合题意;
,符合题意;
当a=﹣ ![]() 时,原方程可化为﹣7x2﹣6x﹣1=0,解得x1=﹣
时,原方程可化为﹣7x2﹣6x﹣1=0,解得x1=﹣ ![]() ,x2=﹣
,x2=﹣ ![]() ,符合题意;
,符合题意;
当a=0时,原方程可化为﹣6x﹣1=0,解得x1=﹣ ![]() ,不符合题意;
,不符合题意;
当a= ![]() 时,原方程可化为7x2﹣6x﹣1=0,解得x1=1,x2=﹣
时,原方程可化为7x2﹣6x﹣1=0,解得x1=1,x2=﹣ ![]() ,符合题意;
,符合题意;
当a=4时,原方程可化为8x2﹣6x﹣1=0,解得x1=﹣ ![]() ,x2=
,x2= ![]() ,符合题意.
,符合题意.
∴取到满足条件的a值的概率= ![]() .
.
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用求根公式和根与系数的关系的相关知识可以得到问题的答案,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
-
科目: 来源: 题型:
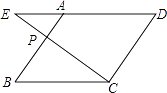
查看答案和解析>>【题目】如图,点P是平行四边形ABCD边AB上一点,且AB=3AP,连接CP,并延长CP、DA交于点E,则△AEP与△DEC的周长之比为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2+4x﹣1=0,下列配方结果正确的是( )
A.(x+2)2=5
B.(x+2)2=1
C.(x﹣2)2=1
D.(x﹣2)2=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一张比例尺为1:5000的地图中,小明家到学校的距离为0.2米,则小明家到学校的实际距离是米.
-
科目: 来源: 题型:
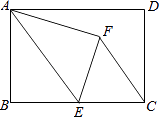
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=12,点E为BC的中点.连接AE,将△ABE沿AE折叠,点B落在点F处,连接CF,现将△CEF绕点E顺时针旋转α角(其中0°≤α≤180°)得到△EC1F1 , 旋转过程中,直线C1F1分别交射线EC、射线AE于点M、N,当EM=EN时,则CM= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母,每空中的字母不重复),请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率;
(2)若在如图三个空格的右侧增加一个空格,将A、B、C、D四个字母任意填写其中(每空填一个字母,每空中的字母不重复),从左往右字母顺序恰好是A、B、C、D的概率为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b是方程x2﹣x﹣3=0的两个根,则代数式a2﹣(a+b)+b2的值为 .
相关试题

