【题目】定义:在平面直角坐标系中,点A、B为函数L图象上的任意两点,点A坐标为(x1,y1),点B坐标为(x2,y2),把式子![]() 称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=
称为函数L从x1到x2的平均变化率;对于函数K:y=2x2﹣3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2﹣x1=![]() 时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=
时,函数K从x1到x2的平均变化率是_____;当x1=1,x2﹣x1=![]() (n为正整数)时,函数K从x1到x2的平均变化率是_____.
(n为正整数)时,函数K从x1到x2的平均变化率是_____.
参考答案:
【答案】![]()
![]()
【解析】
分别求出x1和y1, x2和y2,按定义的运算计算便可.
解:(1)∵x1=1, x2﹣x1=![]() ,
,
∴x2=![]()
∴y1=2×12-3×1+1=0,y2=2×![]() -3×
-3×![]() +1=
+1=![]()
∴函数K从x1到x2的平均变化率是![]() =
=![]() .
.
(2) ∵x1=1, x2﹣x1=![]() ,
,
∴x2=![]()
∴y1=2×12-3×1+1=0,y2=2×![]() -3×
-3×![]() +1=
+1=![]()
∴函数K从x1到x2的平均变化率是![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:(1)函数
 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;(2)下表是x与y的几组对应值.

...





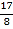

1
2
3
...

...









m
...
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,
 ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数yx3的图象与反比例函数y
 (k为常数,且k0)的图象交于A(1,a),B两点.
(k为常数,且k0)的图象交于A(1,a),B两点.(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程.
(1)x2﹣14x=8(配方法)
(2)x2﹣7x﹣18=0(公式法)
(3)(2x+3)2=4(2x+3)(因式分解法)
(4)2(x﹣3)2=x2﹣9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区2015年投入教育经费2900万元,2017年投入教育经费3509万元.
(1)求2015年至2017年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的情况,该地区到2019年需投入教育经费4250万元.如果按(1)中教育经费投入的增长率,到2019年该地区投入的教育经费是否能达到4250万元?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y1=ax2+c与x轴交于A、B两点,与y轴交于点C,点P在抛物线上,过P(1,﹣3),B(4,0)两点作直线y2=kx+b.
(1)求a、c的值;
(2)根据图象直接写出y1>y2时,x的取值范围;
(3)在抛物线上是否存在点M,使得S△ABP=5S△ABM,若存在,求出点M的坐标,若不存在,请说明理由.

相关试题

