【题目】如图,直线y= ![]() x+6分别与x轴、y轴交于A、B两点:直线y=
x+6分别与x轴、y轴交于A、B两点:直线y= ![]() x与AB于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的进度沿x轴向左运动.过点E作x轴的垂线,分別交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠的图形的周长为L个单位长度,点E的运动时间为t(秒).
x与AB于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的进度沿x轴向左运动.过点E作x轴的垂线,分別交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠的图形的周长为L个单位长度,点E的运动时间为t(秒).
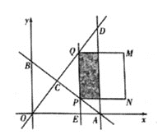
(1)直接写出点C和点A的坐标.
(2)若四边形OBQP为平行四边形,求t的值.
(3)0<t<5时,求L与t之间的函数解析式.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)2;(3)
;(2)2;(3)![]() .
.
【解析】
(1)把y= ![]() x+6和 y=
x+6和 y= ![]() x联立组成方程组,解方程组求得方程组的解,即可得点C的坐标;在直线y=
x联立组成方程组,解方程组求得方程组的解,即可得点C的坐标;在直线y= ![]() x+6中,令y=0,求得x的值,即可得点A的坐标;(2)用t表示出点P、Q的坐标,求得PQ的长,由条件可知,BO∥QP,若使四边形OBQP为平行四边形,必须满足OB=QP,由此可得
x+6中,令y=0,求得x的值,即可得点A的坐标;(2)用t表示出点P、Q的坐标,求得PQ的长,由条件可知,BO∥QP,若使四边形OBQP为平行四边形,必须满足OB=QP,由此可得![]() ,即可求得t值;(3)由题意可知,正方形PQMN与△ACD重叠的图形是矩形,由此求得L与t之间的函数解析式即可.
,即可求得t值;(3)由题意可知,正方形PQMN与△ACD重叠的图形是矩形,由此求得L与t之间的函数解析式即可.
(1)C的坐标为( ![]() ),A的坐标为(8,0);
),A的坐标为(8,0);
(2)∵点B直线y= ![]() x+6与y轴的交点,
x+6与y轴的交点,
∴B(0,6),
∴OB=6,
∵A的坐标为(8,0),
∴OA=8,
由题意可得,OE=8-t,
∴P(8-t,![]() ),Q(8-t,
),Q(8-t,![]() )
)
∴![]() =10-2t,
=10-2t,
由条件可知,BO∥QP,若使四边形OBQP为平行四边形,必须满足OB=QP,
所以有 ![]() ,解得t=2;
,解得t=2;
(3)当0<t<5时, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于任意两点A(x1,y1)B (x2,y2),规定运算:
(1)A⊕B=(x1+x2,y1+y2);
(2)A⊙B=x1x2+y1y2;
(3)当x1=x2且y1=y2时,A=B.
有下列四个命题:
①若有A(1,2),B(2,﹣1),则A⊕B=(3,1),A⊙B=0;
②若有A⊕B=B⊕C,则A=C;
③若有A⊙B=B⊙C,则A=C;
④(A⊕B)⊕C=A⊕(B⊕C)对任意点A、B、C均成立.
其中正确的命题为______(只填序号)
-
科目: 来源: 题型:
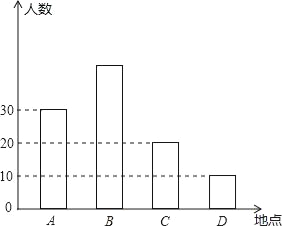
查看答案和解析>>【题目】如图,暑假快要到了,某市准备组织同学们分别到A,B,C,D四个地方进行夏令营活动,前往四个地方的人数.
(1)去B地参加夏令营活动人数占总人数的40%,根据统计图求去B地的人数?
(2)若一对姐弟中只能有一人参加夏令营,姐弟俩提议让父亲决定.父亲说:现有4张卡片上分别写有1,2,3,4四个整数,先让姐姐随机地抽取一张后放回,再由弟弟随机地抽取一张.若抽取的两张卡片上的数字之和是5的倍数则姐姐参加,若抽取的两张卡片上的数字之和是3的倍数则弟弟参加.用列表法或树形图分析这种方法对姐弟俩是否公平?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角
 和坝底宽AD.(结果保留根号)
和坝底宽AD.(结果保留根号)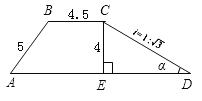
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上有三个点
 、
、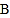 、
、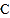 ,如图所示.
,如图所示.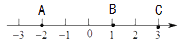
(1)将点
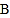 向左平移4个单位,此时该点表示的数是________;
向左平移4个单位,此时该点表示的数是________; (2)将点
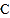 向左平移3个单位得到数
向左平移3个单位得到数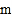 ,再向右平移2个单位得到数
,再向右平移2个单位得到数 ,则
,则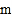 ,
, 分别是多少?
分别是多少? (3)怎样移动
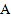 、
、 、
、 中的两点,使三个点表示的数相同?你有几种方法?
中的两点,使三个点表示的数相同?你有几种方法? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OC是∠AOB内一条射线,OD、OE分别是∠AOC、∠BOC的平分线.
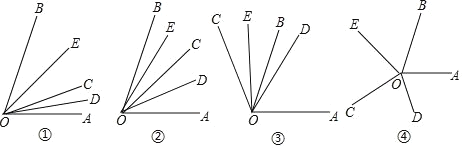
(1)如图①,当∠AOB=80°时,∠DOE=_______°;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠BOE、∠EOD、∠DOA三角之间有怎样的数量关系?并说明理由;
(3)当射线OC在∠AOB外如图③所示位置时,(2)中三个角:∠BOE、∠EOD、∠DOA之间数量关系是_______;
(4)当射线OC在∠AOB外如图④所示位置时,∠BOE、∠EOD、∠DOA之间数量关系是_______.
-
科目: 来源: 题型:
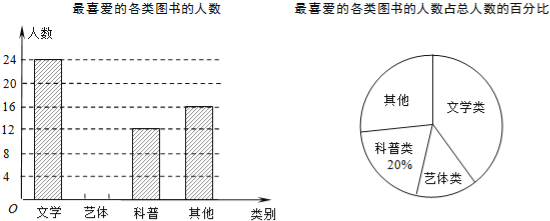
查看答案和解析>>【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
相关试题

