【题目】如图,OC是∠AOB内一条射线,OD、OE分别是∠AOC、∠BOC的平分线.
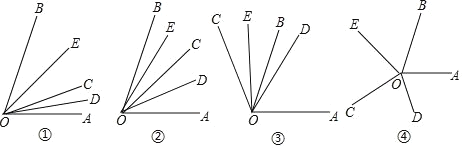
(1)如图①,当∠AOB=80°时,∠DOE=_______°;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠BOE、∠EOD、∠DOA三角之间有怎样的数量关系?并说明理由;
(3)当射线OC在∠AOB外如图③所示位置时,(2)中三个角:∠BOE、∠EOD、∠DOA之间数量关系是_______;
(4)当射线OC在∠AOB外如图④所示位置时,∠BOE、∠EOD、∠DOA之间数量关系是_______.
参考答案:
【答案】(1)40°(2)![]() (3)不成立,理由见解析.(4)∠DOE=∠BOE+∠DOA.
(3)不成立,理由见解析.(4)∠DOE=∠BOE+∠DOA.
【解析】
(1)(2)根据角平分线定义得出∠DOC=![]() ∠AOC,
∠AOC,![]() ,求出∠DOE=
,求出∠DOE=
![]()
![]() ,即可得出答案;
,即可得出答案;
(3)根据角平分线定义得出∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,求出∠DOE=
∠BOC,求出∠DOE=![]() ∠AOC-∠BOC)=
∠AOC-∠BOC)=![]() ∠AOB,即可得出答案;
∠AOB,即可得出答案;
(4)根据角平分线定义即可求解.
当射线OC在∠AOB的内部时,
∵OD,OE分别为∠AOC,∠BOC的角平分线,
∠DOC=![]() ∠AOC,∠EOC=
∠AOC,∠EOC=![]() ∠BOC,
∠BOC,
∴∠DOE=∠DOC+∠EOCP=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB,
∠AOB,
(1)若∠AOB=80°,则∠DOE的度数为40°
故答案为:40;
(2)![]()
(3)当射线OC在∠AOB的外部时(1)中的结论不成立.理由是:
∵OD、OE分别是∠AOC、∠BOC的角平分线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
(4)∵OD,OE分别为∠AOC',∠BOC的角平分线,
![]() ,
,
![]() ,
,
故∠BOE、∠EOD、∠DOA之间数量关系是:
![]()
故答案为:∠DOE=∠BOE+∠DOA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角
 和坝底宽AD.(结果保留根号)
和坝底宽AD.(结果保留根号)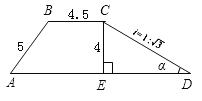
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+6分别与x轴、y轴交于A、B两点:直线y=
x+6分别与x轴、y轴交于A、B两点:直线y=  x与AB于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的进度沿x轴向左运动.过点E作x轴的垂线,分別交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠的图形的周长为L个单位长度,点E的运动时间为t(秒).
x与AB于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的进度沿x轴向左运动.过点E作x轴的垂线,分別交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠的图形的周长为L个单位长度,点E的运动时间为t(秒). 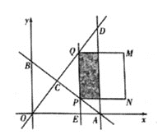
(1)直接写出点C和点A的坐标.
(2)若四边形OBQP为平行四边形,求t的值.
(3)0<t<5时,求L与t之间的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上有三个点
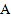 、
、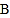 、
、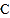 ,如图所示.
,如图所示.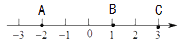
(1)将点
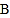 向左平移4个单位,此时该点表示的数是________;
向左平移4个单位,此时该点表示的数是________; (2)将点
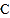 向左平移3个单位得到数
向左平移3个单位得到数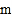 ,再向右平移2个单位得到数
,再向右平移2个单位得到数 ,则
,则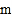 ,
, 分别是多少?
分别是多少? (3)怎样移动
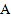 、
、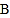 、
、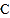 中的两点,使三个点表示的数相同?你有几种方法?
中的两点,使三个点表示的数相同?你有几种方法? -
科目: 来源: 题型:
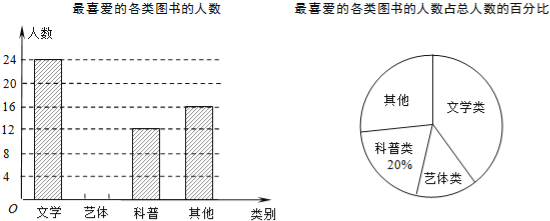
查看答案和解析>>【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
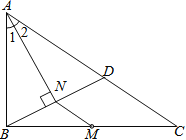
(1)求证:BN=DN;
(2)求△ABC的周长
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲沿周长为300米的环形跑道上按逆时针方向跑步,速度为a米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为t秒.
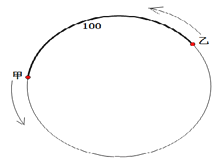
(1)若a=5,求甲、乙两人第1次相遇的时间;
(2)当t=50时,甲、乙两人第1次相遇.
①求a的值;
②若
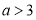 时,甲、乙两人第1次相遇前,当两人相距120米时,求
时,甲、乙两人第1次相遇前,当两人相距120米时,求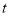 的值.
的值.
相关试题

