【题目】设0!表示自然数由1到n的连乘积,并规定0!=1,Anm=![]() ,nm=
,nm=![]() (n≥0,n≥m)例如1!=1,2!=1×2=2,3!=1×2×3=6,A53=
(n≥0,n≥m)例如1!=1,2!=1×2=2,3!=1×2×3=6,A53=![]() =60,C64=
=60,C64=![]() =15,请回答以下问题:
=15,请回答以下问题:
(1)求C32,A32;
(2)试根据C32,A32,2!的值写出C32,A32,2!满足的等量关系;试根据C43,A43,3!的值写出C43,A43,3!满足的等量关系;试根据C54,A54,4!的值写出C54,A54,4!满足的等量关系;
(3)探究Amn,Cmn与n!之间满足的等量关系(不需要证明).
参考答案:
【答案】(1)3,6;(2)A32=2!C32; A43=3!C43;A54=4!C54;(3)Amn=n!mn.
【解析】
(1)根据题中的新定义计算求出值即可;
(2)利用题中的新定义计算得到所求关系式即可;
(3)归纳总结得到一般性规律,写出即可.
解:(1)根据题中的新定义得:C32=![]() =
=![]() =3,
=3,
A32=![]() =
=![]() =6;
=6;
(2)由C32=3,A32=6,2!=2,得到A32=2!C32;
同理得到:A43=3!C43;A54=4!C54;
(3)∵A32=2!C32;A43=3!C43;A54=4!C54;
归纳总结得:Amn=n!Cmn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图像经过点A(-1,0),并与反比例函数
的图像经过点A(-1,0),并与反比例函数 (
( )的图像交于B(m,4)
)的图像交于B(m,4)
(1)求
 的值;
的值;(2)以AB为一边,在AB的左侧作正方形
 ,求C点坐标;
,求C点坐标;(3)将正方形
 沿着
沿着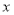 轴的正方向,向右平移n个单位长度,得到正方形
轴的正方向,向右平移n个单位长度,得到正方形 ,线段
,线段 的中点为点
的中点为点 ,若点
,若点 和点
和点 同时落在反比例函数
同时落在反比例函数 的图像上,求n的值.
的图像上,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AE∥CD,CE∥AB.
(1)试判断四边形ADCE的形状,并证明你的结论.
(2)连接BE,若∠BAC=30°,CE=1,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】据新浪网调查,在第十二届全国人大二中全会后,全国网民对政府工作报告关注度非常高,大家关注的热点话题分别有:消费、教育、环保、反腐及其它共五类,且关注五类热点问题的网民的人数所占百分比如图l所示,关注该五类热点问题网民的人数的不完整条形统计如图2,请根据图中信息解答下列问题.
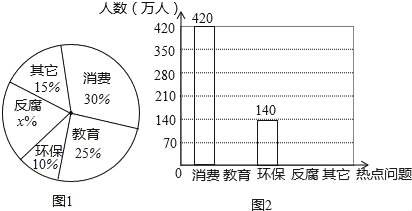
(1)求出图l中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)为了深度了解成都网民对政府工作报告的想法,新浪网邀请成都市5名网民代表甲、乙、丙、丁、戊做客新浪访谈,且一次访谈只选2名代表.请你用列表法或画树状图的方法,求出一次所选代表恰好是丙和丁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是直线AB上的一点,
 是直角,OE平分
是直角,OE平分 .
.(1)如图1.若
 .求
.求 的度数;
的度数;(2)在图1中,
 ,直接写出
,直接写出 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);(3)将图1中的
 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究 和
和 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:点A、B在数轴上分别表示有理数a、b,
 表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①,
表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①, ;
;当A、B两点都在原点右侧时,如图②,
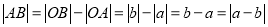 ;
;当AB两点都在原点左侧时,如图③,
 ;
;当AB两点在原点两侧时,如图④,
 ;
;
请根据上述结论,回答下列问题:
(1)数轴上表示2和5的两点问距离是______,数轴上表示2和-6的两点间距高是_________,数轴上表示-1和3的两点间距离是____________.
(2)数轴上表示x和-1的两点A和B之间的距离可表示为_________,若|AB|=2,则x的值为_____________.
(3)当
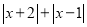 取最小值时,请写出所有符合条件的x的整数值_______________.
取最小值时,请写出所有符合条件的x的整数值_______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200 m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200 m,缆车由点B到点D的行驶路线与水平夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)

相关试题

