搜索
【题目】已知：O是直线AB上的一点，
是直角，OE平分
．
（1）如图1．若
．求
的度数；
（2）在图1中，
，直接写出的度数（用含a的代数式表示）；
（3）将图1中的
绕顶点O顺时针旋转至图2的位置，探究
和的度数之间的关系．写出你的结论，并说明理由．
参考答案：
【答案】（1）
；（2）
；（3）
，理由见解析.
【解析】
（1）先根据补角的定义求出∠BOC的度数，再由角平分线的性质得出∠COE的度数，根据∠DOE=∠COD-∠COE即可得出结论；
（2）同（1）可得出结论；
（3）先根据角平分线的定义得出∠COE=∠BOE=
∠BOC，再由∠DOE=∠COD-∠COE即可得出结论．
（1）∵
是直角，
，
，
，
∵OE平分
，
，
．
（2）
是直角，
，
，
，
∵OE平分，
，
．
（3），
理由是：
，OE平分，
，
，
，
，
即．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校组织学生到距离学校6千米的科技馆去参观，小华因事没能乘上学校的包车，于是准备在学校门口改乘出租车去科技馆，出租车收费标准有两种类型，如下表：
里程
甲类收费（元）
乙类收费（元）
3千米以下（包含3千米）
7.00
6.00
3千米以上，每增加1千米
1.60
1.40
（1）设出租车行驶的里程为x千米（
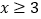且x取正整数），分别写出两种类型的总收费（用含x的代数式表示）；（2）小华身上仅有11元，他乘出租车到科技馆车费够不够请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE.
（1）求证：CE＝AD；
（2）当D为AB中点时，四边形BECD是什么特殊四边形？说明你的理由；
（3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】近两年，国际市场黄金价格涨幅较大，中国交通银行推出“沃德金”的理财产品，即以黄金为投资产品，投资者从黄金价格的上涨中赚取利润．上周五黄金的收盘价为285元/克，下表是本周星期一至星期五黄金价格的变化情况．（注：星期一至星期五开市，星期六.星期日休市）
星期
一
二
三
四
五
收盘价的变化（与前一天收盘价比较）
+7
+5
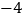
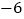
+8
问：（1）本周星期三黄金的收盘价是多少？
（2）本周黄金收盘时的最高价.最低价分别是多少？
（3）上周，小王以周五的收盘价285元/克买入黄金1000克，已知买入与卖出时均需支付成交金额的千分之五的交易费，卖出黄金时需支付成交金额的千分之三的印花税．本周，小王以周五的收盘价全部卖出黄金1000克，他的收益情况如何？
-
科目： 来源： 题型：
查看答案和解析>>【题目】将自然数按如表规律排列，表中数2在第二行第一列，与有序数对
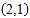对应，数5与
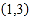对应，数14与
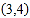对应，根据这一规律，数2014对应的有序数对为__________.第一列
第二列
第三列
第四列
第五列
第一行
1
4
5
16
17
…
第二行
2
3
6
15
…
第三行
9
8
7
14
…
第四行
10
11
12
13
…
第五行
…
……
-
科目： 来源： 题型：
查看答案和解析>>【题目】正方形ABCD的边长为4，将此正方形置于平面直角坐标系中，使AB边落在X轴的正半轴上，且A点的坐标是（1，0）．
（1）直线
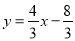经过点C，且与x轴交与点E，求四边形AECD的面积；（2）若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的解析式；
（3）若直线l1经过点F（﹣
，0），且与直线y=3x平行，将（2）中直线l沿着y轴向上平移
个单位交轴x于点M，交直线l1于点N，求△NMF的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校组织学生到距离学校6千米的科技馆去参观，小华因事没能乘上学校的包车，于是准备在学校门口改乘出租车去科技馆，出租车收费标准有两种类型，如下表：
里程
甲类收费（元）
乙类收费（元）
3千米以下（包含3千米）
7.00
6.00
3千米以上，每增加1千米
1.60
1.40
（1）设出租车行驶的里程为x千米（
且x取正整数），分别写出两种类型的总收费（用含x的代数式表示）；（2）小华身上仅有11元，他乘出租车到科技馆车费够不够请说明理由．
相关试题
