【题目】计算:
(1)23﹣17﹣(﹣7)+(﹣16)
(2)![]()
(3)﹣22÷(﹣4)3+|0.8﹣1|×(2![]() )2
)2
(4)4xy+(3y2﹣2x2)﹣(5xy﹣2x2)﹣4y2
(5)先化简,再求值:![]() x﹣2(x﹣y2)+(﹣
x﹣2(x﹣y2)+(﹣![]() x+
x+![]() y2),其中x=﹣
y2),其中x=﹣![]() ,y=3
,y=3
参考答案:
【答案】(1)-3;(2)-26;(3)![]() ;(4)﹣xy﹣y2;(5)﹣3x+
;(4)﹣xy﹣y2;(5)﹣3x+![]() y2,23
y2,23
【解析】
(1)原式利用减法法则,计算即可求出值;(2)原式利用除法法则,再利用乘法分配律计算即可求出值;(3)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可求出值;(4)原式去括号合并即可得到结果;(5)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
解:(1)原式=23﹣17+7﹣16=﹣3;
(2)原式=(![]()
![]() +
+![]() )×36=﹣27﹣20+21=﹣26;
)×36=﹣27﹣20+21=﹣26;
(3)原式=﹣4÷(﹣64)+![]() ×
×![]() =
=![]() +
+![]()
![]()
=![]() ;
;
(4)原4xy+3y2﹣2x2﹣5xy+2x2﹣4y2=﹣xy﹣y2;
(5)原式=![]() x﹣2x+2y2﹣
x﹣2x+2y2﹣![]() x+
x+![]() y2=﹣3x+
y2=﹣3x+![]() y2,
y2,
当x=![]() ,y=3时,原式=2+21=23.
,y=3时,原式=2+21=23.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

-
科目: 来源: 题型:
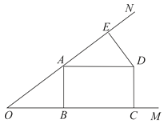
查看答案和解析>>【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因为一次函数y=kx+b与y=-kx+b(k≠0)的图象关于y轴对称,所以我们定义:函数y=kx+b与y=-kx+b(k≠0)互为“镜子”函数.
(1)请直接写出函数y=3x-2的“镜子”函数:______________;
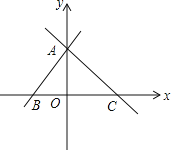
(2)如果一对“镜子”函数y=kx+b与y=-kx+b(k≠0)的图象交于点A,且与x轴交于B、C两点,如图所示,若△ABC是等腰直角三角形,∠BAC=90°,且它的面积是16,求这对“镜子”函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】足球训练中,为了训练球员快速抢断转身,教练设计了折返跑训练.教练在东西方向的足球场上画了一条直线插上不同的折返旗帜,如果约定向西为正,向东为负,练习一组的行驶记录如下(单位:米):+40,-30,+50,-25,+25,-30,+15,-28,+16,-20.
(1)球员最后到达的地方在出发点的哪个方向?距出发点多远?
(2)球员训练过程中,最远处离出发点多远?
(3)球员在一组练习过程中,跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,海中有一小岛P,在距小岛P的
 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
相关试题

