【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

参考答案:
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】分析:(1)先证明△CDE≌△CBF,得到CD=CB,可得ABCD是菱形,则AD=AB,由DE=BF得AE=AF,则△AEF是等边三角形,根据EF的长可得△AEF的面积;
(2)延长DP交BC于N,连结FN,证明△CPN≌△EPD,得到AE=BN,证明△FBN≌△DEF,得到FN=FD,根据等腰三角形三线合一的性质可得结论.
详解:(1)∵四边形ABCD是平行四边形,
∴∠D=∠B,
∵BF=DE,∠DCE=∠BCF,
∴△CDE≌△CBF(AAS),
∴CD=CB,
∴ABCD是菱形,
∴AD=AB,
∴AD﹣DE=AB﹣BF,即AE=AF,
∵∠A=60°,
∴△AEF是等边三角形,
∵EF=2,
∴S△AEF=![]() ×22=
×22=![]() ;
;
(2)证明:如图2,延长DP交BC于N,连结FN,
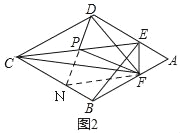
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠EDP=∠PNC,∠DEP=∠PCN,
∵点P是CE的中点,
∴CP=EP.
∴△CPN≌△EPD,
∴DE=CN,PD=PN.
又∵AD=BC.
∴AD﹣DE=BC﹣CN,即AE=BN.
∵△AEF是等边三角形,
∴∠AEF=60°,EF=AE.
∴∠DEF=120°,EF=BN.
∵AD∥BC,
∴∠A+∠ABC=180°,
又∵∠A=60°,
∴∠ABC=120°,
∴∠ABC=∠DEF.
又∵DE=BF,BN=EF.
∴△FBN≌△DEF,
∴DF=NF,
∵PD=PN,
∴PF⊥PD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两条直线AB,CD相交于点O,且∠AOC=∠AOD,射线OM从OB开始绕O点逆时针方向旋转,速度为15°/s,射线ON同时从OD开始绕O点顺时针方向旋转,速度为12°/s,运动时间为t秒(0<t<12,本题出现的角均小于平角)
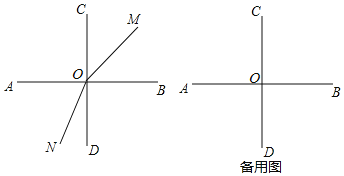
(1)图中一定有 个直角;当t=2时,∠MON的度数为 ,∠BON的度数为 ;
(2)若OE平分∠COM,OF平分∠NOD,当∠EOF为直角时,请求出t的值;
(3)当射线OM在∠COB内部,且
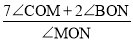 是定值时,求t的取值范围,并求出这个定值.
是定值时,求t的取值范围,并求出这个定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种水果的价格如表:
购买的质量(千克)
不超过10千克
超过10千克
每千克价格
6元
5元
张欣两次共购买了25千克这种水果(第二次多于第一次),共付款132元.问张欣第一次、第二次分别购买了多少千克这种水果?
-
科目: 来源: 题型:
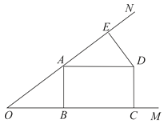
查看答案和解析>>【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长.
-
科目: 来源: 题型:
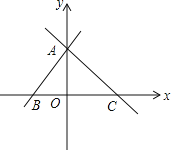
查看答案和解析>>【题目】因为一次函数y=kx+b与y=-kx+b(k≠0)的图象关于y轴对称,所以我们定义:函数y=kx+b与y=-kx+b(k≠0)互为“镜子”函数.
(1)请直接写出函数y=3x-2的“镜子”函数:______________;
(2)如果一对“镜子”函数y=kx+b与y=-kx+b(k≠0)的图象交于点A,且与x轴交于B、C两点,如图所示,若△ABC是等腰直角三角形,∠BAC=90°,且它的面积是16,求这对“镜子”函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)23﹣17﹣(﹣7)+(﹣16)
(2)
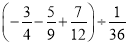
(3)﹣22÷(﹣4)3+|0.8﹣1|×(2
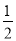 )2
)2(4)4xy+(3y2﹣2x2)﹣(5xy﹣2x2)﹣4y2
(5)先化简,再求值:
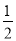 x﹣2(x﹣y2)+(﹣
x﹣2(x﹣y2)+(﹣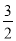 x+
x+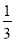 y2),其中x=﹣
y2),其中x=﹣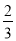 ,y=3
,y=3
相关试题

