搜索
【题目】已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l过点M（1，0），倾斜角为 
． （Ⅰ）求曲线C的直角坐标方程与直线l的参数方程；
（Ⅱ）若曲线C经过伸缩变换 
后得到曲线C′，且直线l与曲线C′交于A，B两点，求|MA|+|MB|．
参考答案：
【答案】解：（Ⅰ）∵曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0，∴ρ2﹣4ρcosθ+3ρ2sin2θ=0， ∴曲线C的直角坐标方程为x2+y2﹣4x+3y2=0，整理，得（x﹣2）2+4y2=4，
∵直线l过点M（1，0），倾斜角为 
，
∴直线l的参数方程为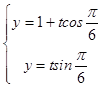 
，即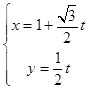 
，（t是参数）．
（Ⅱ）∵曲线C经过伸缩变换 
后得到曲线C′，
∴曲线C′为：（x﹣2）2+y2=4，
把直线l的参数方程 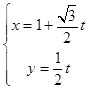，（t是参数）代入曲线C′：（x﹣2）2+y2=4，得：
，
设A，B对应的参数分别为t1 ， t2 ， 则t1+t2= 
，t1t2=﹣3，
∴|MA|+|MB|=|t1|+|t2|=|t1﹣t2|= 
= 
= 
．
【解析】（Ⅰ）曲线C的极坐标方程化为ρ2﹣4ρcosθ+3ρ2sin2θ=0，由此能求出曲线C的直角坐标方程；由直线l过点M（1，0），倾斜角为 
，能求出直线l的参数方程．（Ⅱ）由曲线C经过伸缩变换 
后得到曲线C′，求出曲线C′为：（x﹣2）2+y2=4，把直线l的参数方程代入曲线C′，得： 
，设A，B对应的参数分别为t1 ， t2 ， 则t1+t2= 
，t1t2=﹣3，由此能求出|MA|+|MB|．
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着社会发展，广州市在一天的上下班时段经常会出现堵车严重的现象．交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念．记交通指数为T，其范围为[0，10]，分别有5个级别；T∈[0，2）畅通；T∈[2，4）基本畅通；T∈[4，6）轻度拥堵；T∈[6，8）中度拥堵；T∈[8，10）严重拥堵．早高峰时段（T≥3），从广州市交通指挥中心随机选取了50个交通路段进行调查，依据交通指数数据绘制的直方图如图所示：
（1）据此直方图，估算交通指数T∈[3，9）时的中位数和平均数；
（2）据此直方图，求市区早高峰马路之间的3个路段至少有2个严重拥堵的概率；
（3）某人上班路上所用时间，若畅通时为20分钟，基本畅通为30分钟，轻度拥堵为35分钟；中度拥堵为45分钟；严重拥堵为60分钟，求此人上班所用时间的数学期望． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆E：（x+
）2+y2=16，点F（ ，0），P是圆E上任意一点，线段PF的垂直平分线和半径PE相交于Q．（Ⅰ）求动点Q的轨迹E的方程； （Ⅱ）直线l过点（1，1），且与轨迹Γ交于A，B两点，点M满足 
= 
，点O为坐标原点，延长线段OM与轨迹Γ交于点R，四边形OARB能否为平行四边形？若能，求出此时直线l的方程，若不能，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=ax2﹣（2a﹣1）x﹣lnx（a为常数，a≠0）． （Ⅰ）当a＜0时，求函数f（x）在区间[1，2]上的最大值；
（Ⅱ）记函数f（x）图象为曲线C，设点A（x1 ， y1），B（x2 ， y2）是曲线C上不同的两点，点M为线段AB的中点，过点M作x轴的垂线交曲线C于点N．判断曲线C在点N处的切线是否平行于直线AB？并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=|2x+3|+|2x﹣1|． （Ⅰ）求不等式f（x）＜8的解集；
（Ⅱ）若关于x的不等式f（x）≤|3m+1|有解，求实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列叙述中正确的是（ ）
A.若a，b，c∈R，则“ax2+bx+c≥0”的充分条件是“b2﹣4ac≤0”
B.若a，b，c∈R，则“ab2＞cb2”的充要条件是“a＞c”
C.命题“对任意x∈R，有x2≥0”的否定是“存在x∈R，有x2≥0”
D.l是一条直线，α，β是两个不同的平面，若l⊥α，l⊥β，则α∥β -
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=
，则满足f（f（m））=3f（m）的实数m的取值范围是（ ）
A.（﹣∞，0）∪{﹣
}
B.[0，1]
C.[0，+∞）∪{﹣ }
D.[1，+∞）
相关试题
