搜索
【题目】如图，无人机在空中C处测得地面A、B两点的俯角分别为60°、45°，如果无人机距地面高度CD为
米，点A、D、E在同一水平直线上，则A、B两点间的距离是_____米．（结果保留根号）
参考答案：
【答案】100（1+
）
【解析】如图，利用平行线的性质得∠A=60°，∠B=45°，在Rt△ACD中利用正切定义可计算出AD=100，在Rt△BCD中利用等腰直角三角形的性质得BD=CD=100，然后计算AD+BD即可．
如图，
∵无人机在空中C处测得地面A、B两点的俯角分别为60°、45°，
∴∠A=60°，∠B=45°，
在Rt△ACD中，∵tanA=
，
∴AD=
=100，
在Rt△BCD中，BD=CD=100，
∴AB=AD+BD=100+100=100（1+）．
答：A、B两点间的距离为100（1+）米．
故答案为100（1+）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△PMN中，∠P=90°，PM=PN，MN=6cm，矩形ABCD中AB=2cm，BC=10cm，点C和点M重合，点B、C（M）、N在同一直线上，令Rt△PMN不动，矩形ABCD沿MN所在直线以每秒1cm的速度向右移动，至点C与点N重合为止，设移动x秒后，矩形ABCD与△PMN重叠部分的面积为y，则y与x的大致图象是（ ）
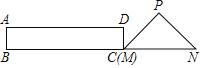
A.
B. 
C. 
D.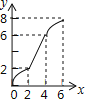 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠AOB的大小为α，P是∠AOB内部的一个定点，且OP＝2，点E、F分别是OA、OB上的动点，若△PEF周长的最小值等于2，则α＝（ ）
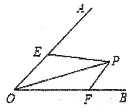
A. 30°B. 45°C. 60°D. 15°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠BAC=90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG平分∠DAC．给出下列结论：①∠BAD=∠C；②AE=AF；③∠EBC=∠C；④FG∥AC；⑤EF=FG．其中正确的结论是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某数学实验小组在探究“关于x的二次三项式ax2+bx+3的性质（a、b为常数）”时，进行了如下活动．
（实验操作）取不同的x的值，计算代数式ax2+bx+3的值．
x
…
﹣1
0
1
2
3
…
ax2+bx+3
…
0
3
4
…
（1）根据上表，计算出a、b的值，并补充完整表格．（观察猜想）实验小组组员，观察表格，提出以下猜想．同学甲说：“代数式ax2+bx+3的值随着x的增大而增大”．同学乙说：“不论x取何值，代数式ax2+bx+3的值一定不大于4”．…
（2）请你也提出一个合理的猜想： （验证猜想）我们知道，猜想有可能是正确的，也可能是错误的．
（3）请你分别判断甲、乙两位同学的猜想是否正确，若不正确，请举出反例；若正确，请加以说理．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠BAC＝90°，点D是BC上一点，将△ABD沿AD翻折后得到△AED，边AE交射线BC于点F．
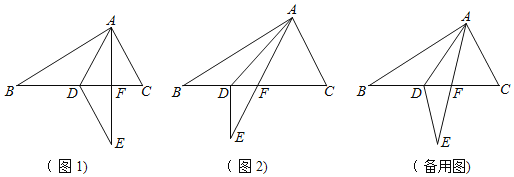
（1）如（图1），当AE⊥BC时，求证：DE∥AC
（2）若∠C＝2∠B，∠BAD＝x°（0＜x＜60）
①如（图2），当DE⊥BC时，求x的值．
②是否存在这样的x的值，使得△DEF中有两个角相等．若存在，并求x的值；若不存在，请说明理由．
-
科目： 来源： 题型：
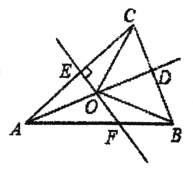
查看答案和解析>>【题目】如图，在△ABC中，AB＝AC，点D是C的中点，AC的垂直平分线分别交AC，AD，AB于点E，O，F.
(1)求证:点O在AB的垂直平分线上;
(2)若∠CAD＝20°，求∠BOF的度数.
相关试题
