【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

参考答案:
【答案】①②④
【解析】
①连接EG.根据等角的余角相等即可得到结果,故①正确;②由BE、AG分别是∠ABC、∠DAC的平分线.得到∠ABF=∠EBD.由于∠AFE=∠FAB+∠FBA,∠AEG=∠C+∠EBD,得到∠AFE=∠AEF,根据等腰三角形的性质可得②正确;③如果∠EBC=∠C,则∠C=![]() ∠ABC,由于∠BAC=90°那么∠C=30°,但∠C≠30°,故③错误;④证明△ABN≌△GBN,得到AN=GN,证出四边形AFGE是平行四边形,得到GF∥AE,故④正确;⑤由AE=AF,AE=FG,而△AEF不是等边三角形,得到EF≠AE,于是EF≠FG,故⑤错误.
∠ABC,由于∠BAC=90°那么∠C=30°,但∠C≠30°,故③错误;④证明△ABN≌△GBN,得到AN=GN,证出四边形AFGE是平行四边形,得到GF∥AE,故④正确;⑤由AE=AF,AE=FG,而△AEF不是等边三角形,得到EF≠AE,于是EF≠FG,故⑤错误.
①连接EG.
∵∠BAC=90°,AD⊥BC.
∴∠C+∠ABC=90°,∠C+∠DAC=90°,∠ABC+∠BAD=90°.
∴∠ABC=∠DAC,∠BAD=∠C,故①正确;
②∵BE、AG分别是∠ABC、∠DAC的平分线,
∴∠ABF=∠EBD.
∵∠AFE=∠FAB+∠FBA,∠AEG=∠C+∠EBD,
∴∠AFE=∠AEF.
∴AF=AE,故②正确;
③如果∠EBC=∠C,则∠C=![]() ∠ABC,
∠ABC,
∵∠BAC=90°,
那么∠C=30°,但∠C≠30°,故③错误;
④∵AG是∠DAC的平分线,
∴AN⊥BE,FN=EN,
在△ABN与△GBN中,∵![]()
∴△ABN≌△GBN.
∴AN=GN.
∴四边形AFGE是平行四边形.
∴GF∥AE.
即GF∥AC.故④正确;
⑤∵AE=AF,AE=FG,
而△AEF不是等边三角形,
∴EF≠AE.
∴EF≠FG,故⑤错误.
故答案为:①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”期间,包河区牛角大圩60亩的秋季花海是游客观赏的首选景点,有着独具一格的农业风情,花海由矮牵牛、孔雀菊、蓝花鼠尾草、一串红等组成。为了种植“花海”,需要从甲乙两地向大圩A.B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A.B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需人民币).
运费(元/吨)
A
B
甲地
12
12
乙地
10
8
(1)设甲地运往
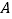 棚营养土
棚营养土 吨,请用关于
吨,请用关于 的代数式完成下表;
的代数式完成下表;运往A.B两地的吨数
A
B
甲地

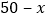
乙地
___
___
(2)设甲地运往A棚营养土
 吨,求总运费
吨,求总运费 (元)关于
(元)关于 (吨)的函数关系式(要求写出自变量取值范围).
(吨)的函数关系式(要求写出自变量取值范围).(3)当甲、乙两地各运往A.B两棚多少吨营养土时,总运费最省?最省的总运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴相交于点A(﹣2,0)和点B,与y轴相交于点C,顶点D(1,﹣
 )
)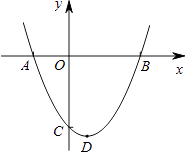
(1)求抛物线对应的函数关系式;
(2)求四边形ACDB的面积;
(3)若平移(1)中的抛物线,使平移后的抛物线与坐标轴仅有两个交点,请直接写出一个平移后的抛物线的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )

A.x<﹣2
B.x>4
C.﹣2<x<4
D.x>0 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.
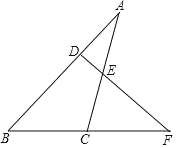
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣4x+3=0.
相关试题

