【题目】如图,已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( )
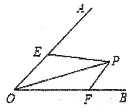
A. 30°B. 45°C. 60°D. 15°
参考答案:
【答案】A
【解析】
设点P关于OA的对称点为C,关于OB的对称点为D,当点E、F在CD上时,△PEF的周长为PE+EF+FP=CD,此时周长最小,根据CD=2可求出α的度数.
如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
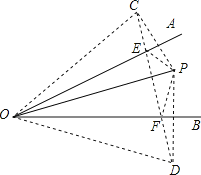
连接OC,OD,PE,PF.
∵点P与点C关于OA对称,
∴OA垂直平分PC,
∴∠COA=∠AOP,PE=CE,OC=OP,
同理,可得∠DOB=∠BOP,PF=DF,OD=OP.
∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB=α,OC=OD=OP=2,
∴∠COD=2α.
又∵△PEF的周长=PE+EF+FP=CE+EF+FD=CD=2,
∴OC=OD=CD=2,
∴△COD是等边三角形,
∴2α=60°,
∴α=30°.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
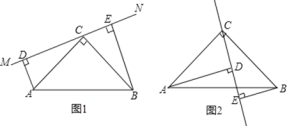
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,则y与x的大致图象是( )
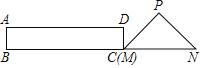
A.
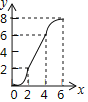 B.
B. 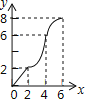 C.
C. 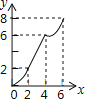 D.
D. 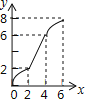
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为
 米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)
米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学实验小组在探究“关于x的二次三项式ax2+bx+3的性质(a、b为常数)”时,进行了如下活动.
(实验操作)取不同的x的值,计算代数式ax2+bx+3的值.
x
…
﹣1
0
1
2
3
…
ax2+bx+3
…
0
3
4
…
(1)根据上表,计算出a、b的值,并补充完整表格.(观察猜想)实验小组组员,观察表格,提出以下猜想.同学甲说:“代数式ax2+bx+3的值随着x的增大而增大”.同学乙说:“不论x取何值,代数式ax2+bx+3的值一定不大于4”.…
(2)请你也提出一个合理的猜想: (验证猜想)我们知道,猜想有可能是正确的,也可能是错误的.
(3)请你分别判断甲、乙两位同学的猜想是否正确,若不正确,请举出反例;若正确,请加以说理.
相关试题

