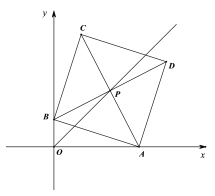
【题目】在平面直角坐标系xOy中,边长为2的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.
(1)如果∠BAO=45°,直接写出点P的坐标;
(2)求证:点P在∠AOB的平分线上;
(3)设点P到x轴的距离为h,直接写出h的取值范围.
参考答案:
【答案】(1)(![]() ,
,![]() );(2)见解析;(3)1<h≤
);(2)见解析;(3)1<h≤![]()
【解析】(1)当∠BAO=45°时,因为四边形ABCD是正方形,P是AC,BD对角线的交点,能证明OAPB是正方形,从而求出P点的坐标.
(2)过P点作x轴和y轴的垂线,可通过三角形全等,证明是角平分线.
(3)因为点P在∠AOB的平分线上,所以h>0,从最小值到最大值时的位置进行分析.
解:(1)∵∠BPA=90°,PA=PB,
∴∠PAB=45°,
∵∠BAO=45°,
∴∠PAO=90°,
∴四边形OAPB是正方形,
∵AB=2,由勾股定理得:PA=PB=![]()
∴P点的坐标为:(![]() ,
,![]() ).
).
(2)证明:作PE⊥y轴于E,PF⊥x轴于F,
∴∠PEB=∠PFA=90°.
∵四边形ABCD是正方形,AC与BD相交于P,
∴PA=PB,∠APB=90°.
∵∠AOB=90°,
∴∠PAO+∠PBO=180°.
∵∠PBE+∠PBO=180°,
∴∠PBE=∠PAO,
在△PEB和△PFA中:

∴△PEB≌和△PFA(AAS)
∴PE=PF
∴OP平分∠AOB.
即无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,
点P都在∠AOB的平分线上;
(3)结合(2)设PF=h,∠APF=α.
在直角△APF中,∠AFP=90°,PA=![]() ,
,
∴PF=PAcosα=![]() cosα,
cosα,
又∵顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),
∴0°≤α<45°,
∴1<h≤![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组,某天乘一辆汽车检修东西走向的“汉施公路”时,约定向东行驶为正,向西行驶为负,他们从A地出发到收工时的行走记录为(单位:千米):-4,+7,-9,+8,+6,-5,+10,-8.
(1)收工时,该小组距离A地多远?
(2) 若汽车行驶每千米耗油0.2升,那么从A地出发到回到A地共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD . 若B(1,0),则点C的坐标为( )
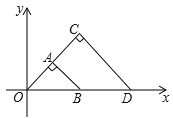
A.(1,2)
B.(1,1)
C.(-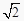 ,-
,- 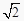 )
)
D.(2,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=
 ,求AB的长。
,求AB的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知含字母m,n的代数式是:
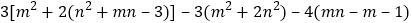 .
.(1)化简这个代数式.
(2)小明取m,n互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0.那么小明所取的字母n的值等于多少?
(3)聪明的小智从化简的代数式中发现,只要字母n取一个固定的数,无论字母m取何数,代数式的值恒为一个不变的数,那么小智所取的字母n的值是多少呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点
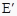 的坐标为( )
的坐标为( ) 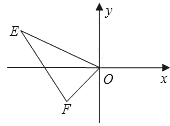
A.(2,-1)或(-2,1)
B.(8,-4)或(-8,4)
C.(2,-1)
D.(8,-4) -
科目: 来源: 题型:
查看答案和解析>>【题目】把2016个正整数1、2、3、4、……、2016按如图方式排列成一个表,用一方框按如图所示的方式任意框住9个数.(方框只能平移)
(1)若框住的9个数中,正中间的一个数为39,则:这九个数的和为__________.
(2)方框能否框住这样的9个数,它们的和等于2016?若能,请写出这9个数;若不能,请说明理由。
(3)若任意框住9个数的和记为S,则:S的最大值与最小值之差等于__________.

相关试题

