【题目】把2016个正整数1、2、3、4、……、2016按如图方式排列成一个表,用一方框按如图所示的方式任意框住9个数.(方框只能平移)
(1)若框住的9个数中,正中间的一个数为39,则:这九个数的和为__________.
(2)方框能否框住这样的9个数,它们的和等于2016?若能,请写出这9个数;若不能,请说明理由。
(3)若任意框住9个数的和记为S,则:S的最大值与最小值之差等于__________.

参考答案:
【答案】(1)351(2)不能框住这样的9个数,它们的和等于2016(3)17991
【解析】
(1)找出所框数字上下两行间的数量关系,左右数字间的数量关系,即可写出另外的八个数,进而求出它们的和;
(2)由(1)可知方框框住这样的9个数的和是正中间的一个数的9倍,代入2016求出中间的数,由224÷7=32,可得出224为32行的第7个数,即2016后面不存在数,从而得出方框框不住这样的9个数.它们的和不能等于2016;
(3)S取最大值时9个数中,正中间的一个数为2008,S取最小值时9个数中,正中间的一个数为3,即可求得S的最大值与最小值,相减即可.
(1)中间一个数是39,则其他八个数分别是31,32,33,38,40,45,46,47,它们的和是351;
﹙2﹚设框住的9数中中间的数为a,则这9数之和为﹙a-8﹚+﹙a-7﹚+﹙a-6﹚+﹙a-1﹚+a+﹙a+1﹚+﹙a+6﹚+﹙a+7﹚+﹙a+8﹚=9a
9a=2016,
a=224,
∵224=7×32,
∴224是表中第32排的最后一个数,
∴不能框住这样的9个数,它们的和等于2016;
(3)S取最大值时9个数中,正中间的一个数为2008,S取最小值时9个数中,正中间的一个数为9,则S最大-S最小=9×2008-9×9=17991,
故答案为:17991
-
科目: 来源: 题型:
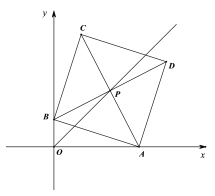
查看答案和解析>>【题目】在平面直角坐标系xOy中,边长为2的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.
(1)如果∠BAO=45°,直接写出点P的坐标;
(2)求证:点P在∠AOB的平分线上;
(3)设点P到x轴的距离为h,直接写出h的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知含字母m,n的代数式是:
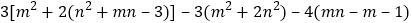 .
.(1)化简这个代数式.
(2)小明取m,n互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0.那么小明所取的字母n的值等于多少?
(3)聪明的小智从化简的代数式中发现,只要字母n取一个固定的数,无论字母m取何数,代数式的值恒为一个不变的数,那么小智所取的字母n的值是多少呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点
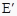 的坐标为( )
的坐标为( ) 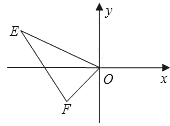
A.(2,-1)或(-2,1)
B.(8,-4)或(-8,4)
C.(2,-1)
D.(8,-4) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B在数轴上表示的数分别为a,b,且|a+6|+(b-18)2=0(规定:数轴上A,B两点之间的距离记为AB).
(1)求b-a的值.
(2)数轴上是否存在点C,使得CA=3CB?若存在,请求出点C所表示的数;若不存在,请说明理由.
(3)动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,动点Q从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,且P比Q先运动2秒.问点Q运动多少秒时,P,Q相距4个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点
 ,
, 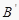 ,
,  .下列说法正确的是( )
.下列说法正确的是( ) 
A.△ 与△ABC是位似图形,位似中心是点(1,0)
与△ABC是位似图形,位似中心是点(1,0)
B.△ 与△ABC是位似图形,位似中心是点(0,0)
与△ABC是位似图形,位似中心是点(0,0)
C.△ 与△ABC是相似图形,但不是位似图形
与△ABC是相似图形,但不是位似图形
D.△ 与△ABC不是相似图形
与△ABC不是相似图形
相关试题

