【题目】如图所示,在△ABC 中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F.
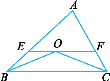
(1)若∠ABC=40°,∠ACB=60°,求∠BOE+∠COF的度数;
(2)若△AEF的周长为8 cm,且BC=4 cm,求△ABC的周长.
参考答案:
【答案】(1)∠BOE+∠COF=50°;(2)12cm.
【解析】
(1)两直线平行,内错角相等,以及根据角平分线性质,可得到![]() 从而求得∠BOE+∠COF的度数.
从而求得∠BOE+∠COF的度数.
(2)根据![]() ,可得△FOC、△EOB均为等腰三角形,由此把△AEF的周长转化为AC+AB,进而可得到△ABC的周长.
,可得△FOC、△EOB均为等腰三角形,由此把△AEF的周长转化为AC+AB,进而可得到△ABC的周长.
解:(1)∵EF∥BC,
∴∠OCB=∠COF,∠OBC=∠BOE.
又∵BO,CO分别是∠BAC和∠ACB的角平分线,
∴∠COF=∠FCO=![]() ∠ACB=30°,∠BOE=∠OBE=
∠ACB=30°,∠BOE=∠OBE=![]() ∠ABC=20°.
∠ABC=20°.
∴∠BOE+∠COF=50°.
(2)∵∠COF=∠FCO,∴OF=CF.
∵∠BOE=∠OBE,∴OE=BE.
∴△AEF的周长=AF+OF+OE+AE=AF+CF+BE+AE=AB+AC=8 cm.
∴△ABC的周长=8+4=12(cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,点
中,点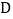 在
在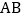 边上,
边上,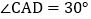 ,
,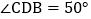 .给出下列三组条件(每组条件中的线段的长度已知):①
.给出下列三组条件(每组条件中的线段的长度已知):①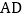 ,
,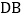 ;②
;②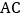 ,
,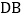 ;③
;③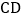 ,
,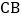 ;能使
;能使 唯一确定的条件的序号为( )
唯一确定的条件的序号为( )
A. ①② B. ①③ C. ②③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )

A.5
B.4
C.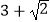
D.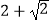
-
科目: 来源: 题型:
查看答案和解析>>【题目】若我们规定三角“
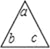 ”表示为:abc;方框“
”表示为:abc;方框“ ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如: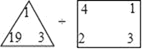 =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:(1)计算:
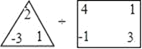 = ______ ;
= ______ ;(2)代数式
 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;(3)解方程:
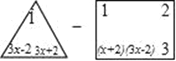 =6x2+7.
=6x2+7. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.
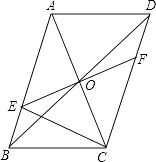
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,求ABCD的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小东设计的“作
 中
中 边上的高线”的尺规作图过程.
边上的高线”的尺规作图过程.已知:
 .
. 求作:
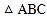 中
中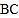 边上的高线
边上的高线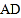 .
.作法:如图,
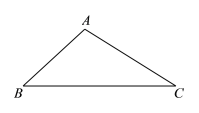
①以点
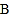 为圆心,
为圆心, 的长为半径作弧,以点
的长为半径作弧,以点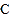 为圆心,
为圆心,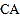 的长为半径作弧,两弧在
的长为半径作弧,两弧在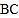 下方交于点
下方交于点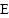 ;
;②连接
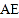 交
交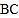 于点
于点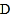 .
.所以线段
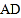 是
是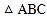 中
中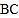 边上的高线.
边上的高线.根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵
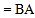 ,
, 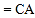 ,
,∴点
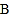 ,
,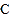 分别在线段
分别在线段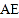 的垂直平分线上( )(填推理的依据).
的垂直平分线上( )(填推理的依据).∴
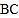 垂直平分线段
垂直平分线段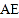 .
. ∴线段
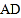 是
是 中
中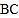 边上的高线.
边上的高线.
相关试题

