【题目】如图,ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.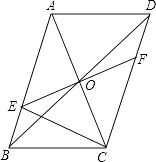
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,求ABCD的周长.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴OD=OB,DC∥AB,
∴∠FDO=∠EBO,
在△DFO和△BEO中, 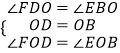 ,
,
∴△DFO≌△BEO(ASA),
∴OE=OF.
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC,
∵EF⊥AC,
∴AE=CE,
∵△BEC的周长是10,
∴BC+BE+CE=BC+BE+AE=BC+AB=10,
∴ABCD的周长=2(BC+AB)=20
【解析】(1)根据平行四边形的性质得OD=OB,DC∥AB,根据平行线的性质得∠FDO=∠EBO,然后利用ASA证出△DFO≌△BEO,利用全等三角形的性质即可得出结论;
(2)根据平行四边形的性质得AB=CD,AD=BC,OA=OC,然后根据中垂线的性质得AE=CE,根据三角形的周长得BC+BE+CE=BC+BE+AE=BC+AB=10,进而得出平行四边形的周长。
【考点精析】通过灵活运用线段垂直平分线的性质和平行四边形的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )

A.5
B.4
C.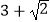
D.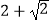
-
科目: 来源: 题型:
查看答案和解析>>【题目】若我们规定三角“
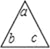 ”表示为:abc;方框“
”表示为:abc;方框“ ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如: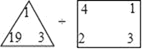 =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:(1)计算:
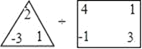 = ______ ;
= ______ ;(2)代数式
 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;(3)解方程:
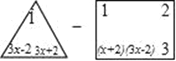 =6x2+7.
=6x2+7. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC 中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F.
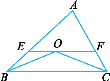
(1)若∠ABC=40°,∠ACB=60°,求∠BOE+∠COF的度数;
(2)若△AEF的周长为8 cm,且BC=4 cm,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小东设计的“作
 中
中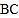 边上的高线”的尺规作图过程.
边上的高线”的尺规作图过程.已知:
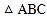 .
. 求作:
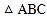 中
中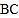 边上的高线
边上的高线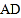 .
.作法:如图,
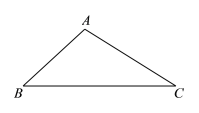
①以点
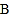 为圆心,
为圆心, 的长为半径作弧,以点
的长为半径作弧,以点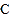 为圆心,
为圆心,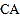 的长为半径作弧,两弧在
的长为半径作弧,两弧在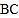 下方交于点
下方交于点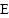 ;
;②连接
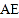 交
交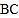 于点
于点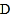 .
.所以线段
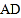 是
是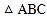 中
中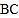 边上的高线.
边上的高线.根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵
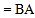 ,
, 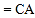 ,
,∴点
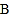 ,
,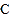 分别在线段
分别在线段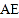 的垂直平分线上( )(填推理的依据).
的垂直平分线上( )(填推理的依据).∴
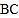 垂直平分线段
垂直平分线段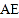 .
. ∴线段
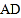 是
是 中
中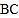 边上的高线.
边上的高线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AOB是一钢架,且∠AOB=10 °,为使钢架更加坚固,需在其内部添加一些钢管EF、FG、GH……添加的钢管长度都与OE相等,则最多能添加这样的钢管( )根。
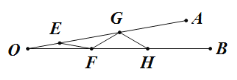
A. 7根 B. 8根 C. 9根 D. 10根
相关试题

