【题目】如图(1)△ABC中,H是高AD和BE的交点,且AD=BD.
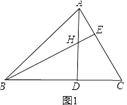
(1)请你猜想BH和AC的关系,并说明理由;
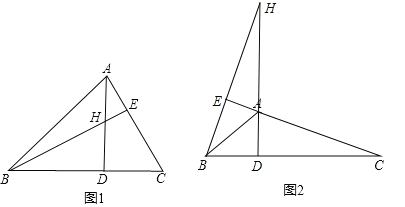
(2)若将图(1)中的∠A改成钝角,请你在图(2)中画出该题的图形,此时(1)中的结论还成立吗?(不必证明).

参考答案:
【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】(1)BH=AC;证明△BDH≌△ADC即可;
(2)成立.证明思路同(1).
(1)BH=AC;如图1.
∵AD和BE是△ABC的高,∴∠BDH=∠ADC=90°,∠DBH+∠C=∠CAD+∠C=90°,∴∠DBH=∠DAC.在△BDH和△ADC中,∵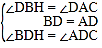 ,∴△BDH≌△ADC(ASA),∴BH=AC;
,∴△BDH≌△ADC(ASA),∴BH=AC;
(2)成立,如图2.
∵AD和BE是△ABC的高,∴∠BDH=∠ADC=90°,∠DBH+∠H=∠DBH+∠C=90°,∴∠H=∠C.在△BDH和△ADC中,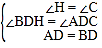 ,∴△BDH≌△ADC(AAS),∴BH=AC.
,∴△BDH≌△ADC(AAS),∴BH=AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形
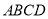 中,
中,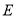 、
、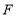 是对角线
是对角线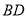 上不同的两点,下列条件中,不能得到四边形
上不同的两点,下列条件中,不能得到四边形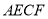 一定为平行四边形的是( )
一定为平行四边形的是( )A.
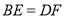 B.
B.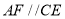 C.
C.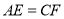 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京昌平临川学校政教处刘颖华主任为初二女学生安排住宿,如果每间住4人,那么将有30人无法安排,如果每间住8人,那么有一间宿舍不空也不满.求宿舍间数和初二女学生人数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】热气球的探测器显示,从热气球A看一栋高楼顶部B处的仰角为30,看这栋高楼底部C处的俯角为60,若热气球与高楼的水平距离为90 m,则这栋高楼有多高?(结果保留整数,
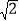 ≈1.414,
≈1.414,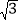 ≈1.732)
≈1.732)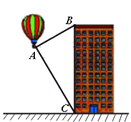
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示.

(1)若DF=2,求AB的长;
(2)若AB=18时,等边△CDP和△EFP的面积之和是否有最大值,如果有最大值,求最大值及此时P点位置,若没有最大值,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,在
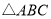 中,
中, 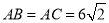 ,
,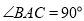 ,点
,点 、
、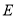 为
为 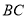 边上两点, 将
边上两点, 将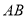 、
、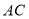 分别沿
分别沿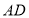 、
、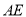 折叠,
折叠,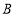 、
、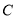 两点重合于点
两点重合于点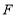 ,若
,若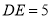 ,则
,则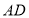 的长为__________.
的长为__________.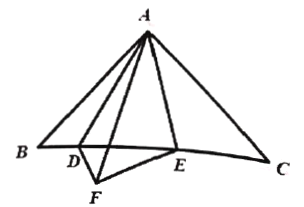
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形(非正方形)四个内角的平分线围成的四边形是__________形.(埴特殊四边形)
相关试题

