【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
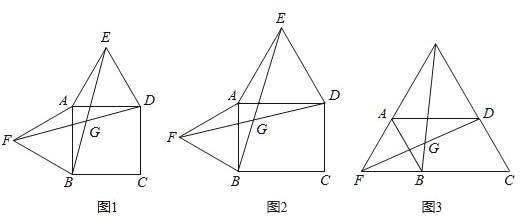
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
参考答案:
【答案】(1)EB=FD;(2)EB=FD,证明见解析;(3)不变,∠EGD=60°
【解析】试题分析:(1)EB=FD,利用正方形的性质、等边三角形的性质和全等三角形的证明方法可证明△AFD≌△ABE,由全等三角形的性质即可得到EB=FD;
(2)当四边形ABCD为矩形时,EB和FD仍旧相等,证明的思路同(1);
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD不发生变化,是一定值,为60°.
试题解析:
(1)EB=FD,
理由如下:
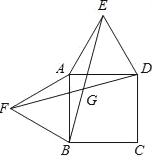
∵四边形ABCD为正方形,
∴AB=AD,
∵以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,
∴AF=AE,∠FAB=∠EAD=60°,
∵∠FAD=∠BAD+∠FAB=90°+60°=150°,
∠BAE=∠BAD+∠EAD=90°+60°=150°,
∴∠FAD=∠BAE,
在△AFD和△ABE中,
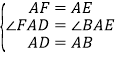 ,
,
∴△AFD≌△ABE,
∴EB=FD;
(2)EB=FD.
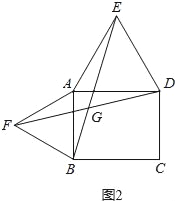
证:∵△AFB为等边三角形
∴AF=AB,∠FAB=60°
∵△ADE为等边三角形,
∴AD=AE,∠EAD=60°
∴∠FAB+∠BAD=∠EAD+∠BAD,
即∠FAD=∠BAE
∴△FAD≌△BAE
∴EB=FD;
(3)解:
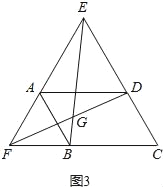
同(2)易证:△FAD≌△BAE,
∴∠AEB=∠ADF,
设∠AEB为x°,则∠ADF也为x°
于是有∠BED为(60﹣x)°,∠EDF为(60+x)°,
∴∠EGD=180°﹣∠BED﹣∠EDF
=180°﹣(60﹣x)°﹣(60+x)°
=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】运用等式性质进行的变形,不正确的是( )
A.如果a=b,那么a﹣c=b﹣c
B.如果a=b,那么a+c=b+c
C.如果a=b,那么ac=bc
D.如果ac=bc,那么a=b -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABF中,C为AF上一点且AB=AC.
(1)尺规作图:作出以AB为直径的⊙O,⊙O分别交AC、BC于点D、E,在图上标出D、E,在图上标出D、E(保留作图痕迹,不写作法).
(2)若∠BAF=2∠CBF,求证:直线BF是⊙O的切线;
(3)在(2)中,若AB=5,sin∠CBF=
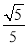 ,求BC和BF的长.
,求BC和BF的长.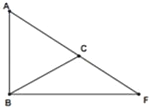
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=6.M、N分别是AB、CD边的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】己知反比例函数:y=
 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).(1)分别求反比例函数和一次函数的解析式;
(2)若M(x1,y1)、N(x2,y2)是反比例函数y=
 图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,若∠A:∠B=2:3,则∠C=______度,∠D=______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李刚家去年养殖的“丰收一号”多宝鱼喜获丰收,上市20天全部售完,李刚对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,多宝鱼价格z(单位:元/件)与上市时间x(单位:天)的函数关系如图2所示.
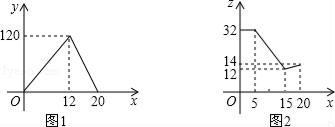
(1)观察图象,直接写出日销售量的最大值;
(2)求李刚家多宝鱼的日销售量y与上市时间x的函数解析式;
(3)试比较第10天与第12天的销售金额哪天多?
相关试题

