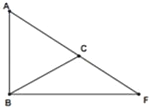
【题目】在△ABF中,C为AF上一点且AB=AC.
(1)尺规作图:作出以AB为直径的⊙O,⊙O分别交AC、BC于点D、E,在图上标出D、E,在图上标出D、E(保留作图痕迹,不写作法).
(2)若∠BAF=2∠CBF,求证:直线BF是⊙O的切线;
(3)在(2)中,若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
参考答案:
【答案】(1)作图见解析;(2)证明见解析;(3)BC=2![]() ,BF=
,BF=![]() .
.
【解析】试题分析:(1)作AB的垂直平分线交AB于O,以O为圆心,OA为半径作圆,⊙O即为所求;
(2)根据圆周角定理得到∠AEB=90°,根据等腰三角形的性质得到∠1=![]() ∠CAB,等量代换得到∠1=∠CBF,求出∠CBF+∠2=90°,然后,根据切线的判定即可得到结论;
∠CAB,等量代换得到∠1=∠CBF,求出∠CBF+∠2=90°,然后,根据切线的判定即可得到结论;
(3)根据已知条件得到sin∠1=![]() ,求出BE=ABsin∠1=
,求出BE=ABsin∠1=![]() ,根据勾股定理得到BC=2BE=2
,根据勾股定理得到BC=2BE=2![]() ,由勾股定理得AE=
,由勾股定理得AE=![]() =2
=2![]() ,于是得到sin∠2=
,于是得到sin∠2=![]() ,cos∠2=
,cos∠2=![]() ,根据三角函数的定义得到AG=3,根据相似三角形的性质即可得到结论.
,根据三角函数的定义得到AG=3,根据相似三角形的性质即可得到结论.
试题解析:(1)如图1,所示⊙O为所求作的圆;
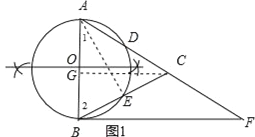
(2)连结AE,
∵AB是⊙O的直径,∴∠AEB=90°,∴∠1+∠2=90°,
∵AB=AC,∴∠1=![]() ∠CAB,
∠CAB,
∵∠BAF=2∠CBF,∴∠CBF=![]() CAB,∴∠1=∠CBF,∴∠CBF+∠2=90°,
CAB,∴∠1=∠CBF,∴∠CBF+∠2=90°,
∵即∠ABF=90°,∵AB是⊙O的直径,
∴直线BF是⊙O的切线;
(3)过点C作CG⊥AB于点G,
∵sin∠CBF=![]() ,∠1=∠CBF,∴sin∠1=
,∠1=∠CBF,∴sin∠1=![]() ,
,
∵∠AEB=90°,AB=5,∴BE=ABsin∠1=![]() ,
,
∵AB=AC,∠AEB=90°,∴BC=2BE=2![]() ,
,
在Rt△ABE中,由勾股定理得AE=![]() =2
=2![]() ,∴sin∠2=
,∴sin∠2=![]() ,cos∠2=
,cos∠2=![]() ,
,
在Rt△CBG中,GC=BC sin∠2=2![]() ×
×![]() =4,GB=BCcos∠2=2,∴AG=3,
=4,GB=BCcos∠2=2,∴AG=3,
∵GC∥BF,∴△AGC∽△ABF,∴![]() ,∴BF=
,∴BF=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A(0,4),B(3,0),以AB为边在第一象限内作正方形ABCD,直线L:y=kx+3.
(1)当直线l经过D点时,求点D的坐标及k的值;
(2)当直线L与正方形有两个交点时,直接写出k的取值范围.
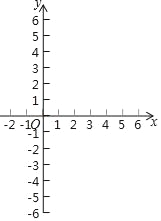
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.
(1)求该抛物线的解析式及点D的坐标;
(2)连接AC,CD,BD,BC,设△AOC、△BOC、△BCD的面积分别为S1,S2和S3,求证:S3=
 ;
;(3)点M是线段AB上一动点(不包括点A和点B),过点M作MN∥BC交AC于点N,连接MC,是否存在点M使∠AMN=∠ACM?若存在,求出点M的坐标和此时直线MN的解析式;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】运用等式性质进行的变形,不正确的是( )
A.如果a=b,那么a﹣c=b﹣c
B.如果a=b,那么a+c=b+c
C.如果a=b,那么ac=bc
D.如果ac=bc,那么a=b -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=6.M、N分别是AB、CD边的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
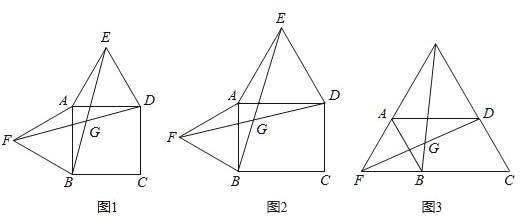
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知反比例函数:y=
 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).(1)分别求反比例函数和一次函数的解析式;
(2)若M(x1,y1)、N(x2,y2)是反比例函数y=
 图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由.
相关试题

