【题目】己知反比例函数:y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)分别求反比例函数和一次函数的解析式;
(2)若M(x1,y1)、N(x2,y2)是反比例函数y=![]() 图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M,N各位于哪个象限,并简要说明理由.
参考答案:
【答案】(1)反比例函数的解析式为y=![]() ,一次函数的解析式为y=2x+6;(2)M(x1,y1)在第三象限,N(x2,y2)在第一象限.
,一次函数的解析式为y=2x+6;(2)M(x1,y1)在第三象限,N(x2,y2)在第一象限.
【解析】试题分析:(1)由点A的坐标结合反比例函数图象上点的坐标特征即可求出反比例函数的解析式;再利用反比例函数图象上点的坐标特征求出点B的坐标,再由A、B的坐标利用待定系数法即可求出一次函数解析式;
(2)由k1的值结合反比例函数的性质即可分析出点M、N所在的象限.
试题解析:(1)∵反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m),
与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m),
∴k1=1×8=8,
∴反比例函数的解析式为y=![]() ,
,
∵﹣4m=8,解得:m=﹣2,
∴点B的坐标为(﹣4,﹣2),
把A(1,8)、B(﹣4,﹣2)代入一次函数y=k2x+b中,
得![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为y=2x+6;
(2)∵反比例函数y=![]() 的图象位于一、三象限,
的图象位于一、三象限,
∴在每个象限内,y随x的增大而减小,
∵x1<x2,y1<y2,
∴M,N在不同的象限,
∴M(x1,y1)在第三象限,N(x2,y2)在第一象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABF中,C为AF上一点且AB=AC.
(1)尺规作图:作出以AB为直径的⊙O,⊙O分别交AC、BC于点D、E,在图上标出D、E,在图上标出D、E(保留作图痕迹,不写作法).
(2)若∠BAF=2∠CBF,求证:直线BF是⊙O的切线;
(3)在(2)中,若AB=5,sin∠CBF=
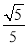 ,求BC和BF的长.
,求BC和BF的长.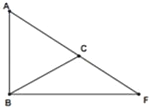
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=6.M、N分别是AB、CD边的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
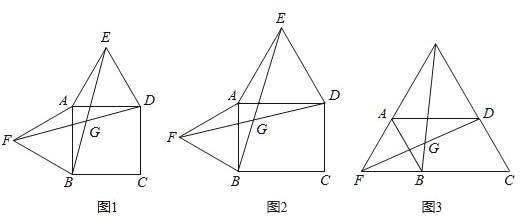
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,若∠A:∠B=2:3,则∠C=______度,∠D=______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李刚家去年养殖的“丰收一号”多宝鱼喜获丰收,上市20天全部售完,李刚对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,多宝鱼价格z(单位:元/件)与上市时间x(单位:天)的函数关系如图2所示.
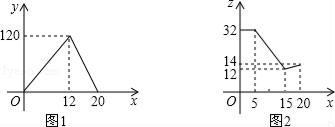
(1)观察图象,直接写出日销售量的最大值;
(2)求李刚家多宝鱼的日销售量y与上市时间x的函数解析式;
(3)试比较第10天与第12天的销售金额哪天多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】等式2x-y=10变形为-4x+2y=-20的依据为( )
A. 等式的基本性质1B. 等式的基本性质2
C. 分数的基本性质D. 分配律
相关试题

