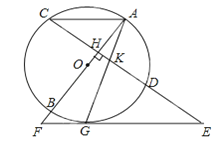
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于切点为G,连接AG交CD于K.
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=
,AK=![]() ,求FG的长.
,求FG的长.
参考答案:
【答案】(1)证明见解析;(2)AC∥EF,证明见解析;(3)FG= ![]() .
.
【解析】试题分析:(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;
(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KDGE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;
(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.
试题解析:(1)如图1,连接OG.
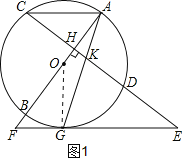
∵EG为切线,
∴∠KGE+∠OGA=90°,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
(2)AC∥EF,理由为连接GD,如图2所示.
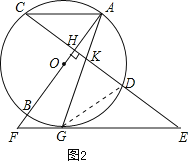
∵KG2=KDGE,即![]() ,
,
∴![]() ,
,
又∵∠KGE=∠GKE,
∴△GKD∽△EGK,
∴∠E=∠AGD,
又∵∠C=∠AGD,
∴∠E=∠C,
∴AC∥EF;
(3)连接OG,OC,如图3所示,
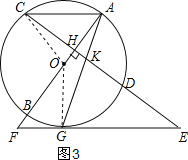
∵EG为切线,
∴∠KGE+∠OGA=90°,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
∵sinE=sin∠ACH=![]()
,设AH=3t,则AC=5t,CH=4t,
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK-CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=(2![]() )2,解得t=
)2,解得t=![]() .
.
设⊙O半径为r,在Rt△OCH中,OC=r,OH=r-3t,CH=4t,
由勾股定理得:OH2+CH2=OC2,
即(r-3t)2+(4t)2=r2,解得r=![]() t=
t=![]() .
.
∵EF为切线,
∴△OGF为直角三角形,
在Rt△OGF中,OG=r=![]() ,tan∠OFG=tan∠CAH=
,tan∠OFG=tan∠CAH=![]() ,
,
∴FG=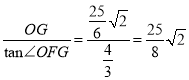
-
科目: 来源: 题型:
查看答案和解析>>【题目】据招商引资网消息,为加快新区经济发展,新区政府拟新区现代高效农业示范园区,共计划投入资金3.75亿元,精确到千万位可表示为( )
A.3.7×108
B.3.8×108
C.0.38×1010
D.37×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】a、b、c是同一平面内的任意三条直线,其交点有( )
A. 1或2个
B. 1或2或3个
C. 0或1或3个
D. 0或1或2或3个
-
科目: 来源: 题型:
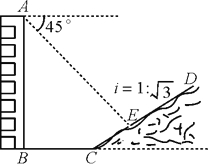
查看答案和解析>>【题目】如图,一楼房AB后有一假山,其坡度为i=1∶
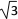 ,山坡坡面上E点处有一休息亭,测
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角
为45°,求楼房AB的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB =90°,∠ABC=30°,将△ABC绕点C顺时针旋转
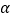 角(0°<
角(0°< 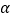 <180°)至△A′B′C , 使得点A′恰好落在AB边上,则
<180°)至△A′B′C , 使得点A′恰好落在AB边上,则 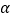 等于( ).
等于( ).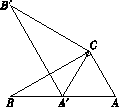
A.150°
B.90°
C.60°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点
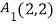 在直线
在直线  上,过点
上,过点 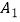 作
作 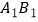 ∥y轴,交直线
∥y轴,交直线 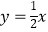 于点
于点 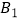 ,以
,以 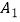 为直角顶点,
为直角顶点, 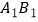 为直角边,在
为直角边,在 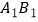 的右侧作等腰直角三角形
的右侧作等腰直角三角形  ;再过点
;再过点 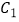 作
作 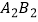 ∥y轴,分别交直线
∥y轴,分别交直线  和
和 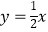 于
于 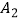 ,
, 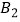 两点,以
两点,以 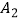 为直角顶点,
为直角顶点, 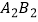 为直角边,在
为直角边,在 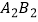 的右侧作等腰直角三角形
的右侧作等腰直角三角形  ,…,按此规律进行下去,点
,…,按此规律进行下去,点 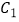 的横坐标为 , 点
的横坐标为 , 点  的横坐标为 , 点
的横坐标为 , 点  的横坐标为 . (用含n的式子表示,n为正整数)
的横坐标为 . (用含n的式子表示,n为正整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2+6x﹣3=0,原方程可变形为( )
A.(x+3)2=9B.(x+3)2=12C.(x+3)2=15D.(x+3)2=39
相关试题

