【题目】如图,在平面直角坐标系xOy中,点 ![]() 在直线
在直线 ![]() 上,过点
上,过点 ![]() 作
作 ![]() ∥y轴,交直线
∥y轴,交直线 ![]() 于点
于点 ![]() ,以
,以 ![]() 为直角顶点,
为直角顶点, ![]() 为直角边,在
为直角边,在 ![]() 的右侧作等腰直角三角形
的右侧作等腰直角三角形 ![]() ;再过点
;再过点 ![]() 作
作 ![]() ∥y轴,分别交直线
∥y轴,分别交直线 ![]() 和
和 ![]() 于
于 ![]() ,
, ![]() 两点,以
两点,以 ![]() 为直角顶点,
为直角顶点, ![]() 为直角边,在
为直角边,在 ![]() 的右侧作等腰直角三角形
的右侧作等腰直角三角形 ![]() ,…,按此规律进行下去,点
,…,按此规律进行下去,点 ![]() 的横坐标为 , 点
的横坐标为 , 点 ![]() 的横坐标为 , 点
的横坐标为 , 点 ![]() 的横坐标为 . (用含n的式子表示,n为正整数)
的横坐标为 . (用含n的式子表示,n为正整数)
参考答案:
【答案】3;![]() ;
;![]()
【解析】解:∵点 ![]() 在直线
在直线 ![]() 上,过点
上,过点 ![]() 作
作 ![]() ∥y轴,交直线
∥y轴,交直线 ![]() 于点
于点 ![]() ,
,
∴B1(2,1),
∴A1C1= A1B1=1,
∴C1(3,2).
∵A2B2∥y ,
∴A2(3,3), ![]() ,
,
∴A2C2= A2B2= ![]() ,
, ![]()
![]()
![]() ,即
,即 ![]() .
.
∵A3B3∥y , ![]() ,
, ![]() ,
,
∴A3C3= A3B3= ![]() ,
, ![]()
![]() ,即
,即 ![]() .
.
∴C1的横坐标为![]() ;
;
C2的横坐标为 ![]() ;
;
C3的横坐标为 ![]() ;
;
……
∴Cn的横坐标为 ![]() .
.
【考点精析】掌握数与式的规律和等腰直角三角形是解答本题的根本,需要知道先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律;等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.
-
科目: 来源: 题型:
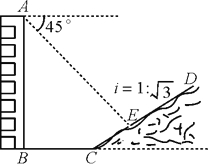
查看答案和解析>>【题目】如图,一楼房AB后有一假山,其坡度为i=1∶
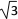 ,山坡坡面上E点处有一休息亭,测
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角
为45°,求楼房AB的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于切点为G,连接AG交CD于K.
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE=
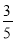 ,AK=
,AK=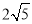 ,求FG的长.
,求FG的长.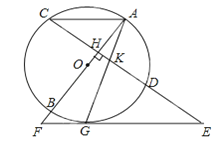
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB =90°,∠ABC=30°,将△ABC绕点C顺时针旋转
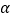 角(0°<
角(0°< 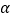 <180°)至△A′B′C , 使得点A′恰好落在AB边上,则
<180°)至△A′B′C , 使得点A′恰好落在AB边上,则 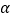 等于( ).
等于( ).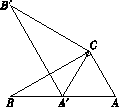
A.150°
B.90°
C.60°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2+6x﹣3=0,原方程可变形为( )
A.(x+3)2=9B.(x+3)2=12C.(x+3)2=15D.(x+3)2=39
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数
 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.(1)求k的值;
(2)点N(a,1)是反比例函数
 (x>0)图象上的点在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学实践探究活动中,大家遇到了这样的问题:
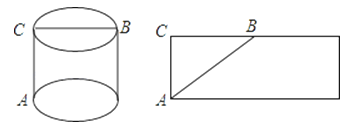
如图,在一个圆柱体形状的包装盒的底部A处有一只壁虎,在顶部B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?
楠楠同学设计的方案是壁虎沿着A﹣C﹣B爬行;
浩浩同学设计的方案是将包装盒展开,在侧面展开图上连接AB,然后壁虎在包装盒的表面上沿着AB爬行.
在这两位同学的设计中,哪位同学的设计是最短路线呢?他们的理论依据是什么?( )
A. 楠楠同学正确,他的理论依据是“直线段最短”
B. 浩浩同学正确,他的理论依据是“两点确定一条直线”
C. 楠楠同学正确,他的理论依据是“垂线段最短”
D. 浩浩同学正确,他的理论依据是“两点之间,线段最短”
相关试题

