【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O与边AB,BC分别交于点D,E.过E的直线与⊙O相切,与AC的延长线交于点G,与AB交于点F.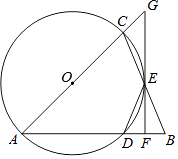
(1)求证:△BDE为等腰三角形;
(2)求证:GF⊥AB;
(3)若⊙O半径为3,DF=1,求CG的长.
参考答案:
【答案】
(1)证明:∵四边形ACED是⊙O的内接四边形,
∴∠ACB+∠ADE=180°,
∵∠BDE+∠ADE=180°,
∴∠BDE=∠ACB,
∵AB=AC,
∴∠B=∠ACB.
∴∠B=∠BDE,
∴△BDE为等腰三角形
(2)证明:连结OE,
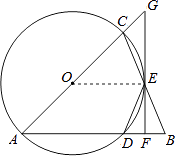
∵直线FG与⊙O相切,
∴∠OEG=90°,
∵OC=OE,
∴∠OEC=∠ACB,
∵∠B=∠ACB,
∴∠B=∠OEC,
∴OE∥AB,
∴∠AFG=∠OEG=90°,
即GF⊥AB
(3)解:设CG=x.
∵△BDE为等腰三角形,GF⊥AB,
∴BF=DF=1,AF=AB﹣BF=AC﹣BF=5,
∵OE∥AB,
∴△GOE∽△GAF,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得x= ![]() ,
,
即CG= ![]() .
.
【解析】(1)由四边形ACED是⊙O的内接四边形,得到∠ACB+∠ADE=180°,由于∠BDE+∠ADE=180°,得到∠BDE=∠ACB,即可得到结论;
(2)连结OE,根据切线的性质得到∠OEG=90°,根据等腰三角形的性质得到∠OEC=∠ACB,根据平行线的性质即可得到结论
(3)设CG=x.根据等腰三角形的性质得到BF=DF=1,AF=AB-BF=AC-BF=5,由相似三角形的判定和性质即可得到结论.
【考点精析】通过灵活运用等腰三角形的性质和圆内接四边形的性质,掌握等腰三角形的两个底角相等(简称:等边对等角);把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形即可以解答此题.
-
科目: 来源: 题型:
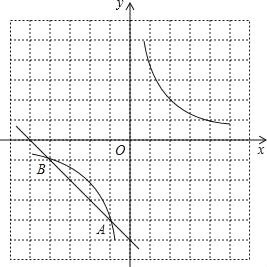
查看答案和解析>>【题目】如图,在方格纸中(小正方形的边长为1),反比例函数的图象与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)求这个反比例函数的解析式;
(2)若点C在已知的反比例函数的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(4﹣n,﹣4)是直线y=kx+b和双曲线y=
 的两个交点.
的两个交点.(1)求两个函数的表达式;
(2)观察图象,直接写出不等式kx+b﹣
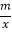 ≥0的解集.
≥0的解集.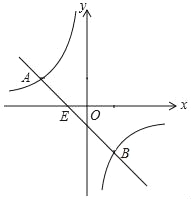
-
科目: 来源: 题型:
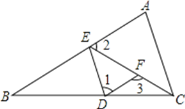
查看答案和解析>>【题目】如图,已知:∠A=∠1,∠2+∠3=180°,∠BDE=65°,
(1)AB与DF平行吗?说明理由;
(2)求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
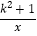 的图上象有三个点(2,y1),(3,y2),(﹣1,y3),则y1,y2,y3的大小关系是( )
的图上象有三个点(2,y1),(3,y2),(﹣1,y3),则y1,y2,y3的大小关系是( )A. y1>y2>y3B. y2>y1>y3C. y3>y1>y2D. y3>y2>y1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E,F分别是AC,AB边上点,连接EF,将纸片ACB的一角沿EF折叠.
(1)如图①,若折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△AEF , 则AE=;
(2)如图②,若折叠后点A落在BC边上的点M处,且使MF∥CA.求AE的长;
(3)如图③,若折叠后点A落在BC延长线上的点N处,且使NF⊥AB.求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与x轴、y轴分别交于点A,B,另一直线
与x轴、y轴分别交于点A,B,另一直线 与x轴、y轴分别交于点C,D,两直线相交于点M.
与x轴、y轴分别交于点C,D,两直线相交于点M. 求点M的坐标;
求点M的坐标; 连接AD,求△AMD的面积.
连接AD,求△AMD的面积.
相关试题

