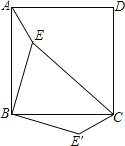
【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C= 度.
参考答案:
【答案】135
【解析】
试题分析:首先根据旋转的性质得出,△EBE′是直角三角形,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
解:连接EE′
∵△ABE绕点B顺时针旋转90°到△CBE′
∴∠EBE′是直角,∴△EBE′是直角三角形,
∵△ABE与△CE′B全等
∴BE=BE′=2,∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°,
∵EE′2=22+22=8,AE=CE′=1,EC=3,
∴EC2=E′C2+EE′2,
∴△EE′C是直角三角形,
∴∠EE′C=90°,
∴∠AEB=135°.
故答案为:135.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若已知x+y=3,xy=1,试求(1) (x-y)2 的值 (2)x3y+xy3的值..
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明发明了一个魔术盒,当任意实数对(a,b)进入其中时,会得到一个新的实数:a2+b﹣1,例如把(3,﹣2)放入其中,就会得到32+(﹣2)﹣1=6.那么如果将实数对(m,﹣2m)放入其中,得到实数2,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的内角和等于360度,那么这个多边形的边数为( )
A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 三角形的内心到三角形的三个顶点的距离相等 B. 三点确定一个圆
C. 垂直于半径的直线一定是这个圆的切线 D. 任何三角形有且只有一个内切圆
-
科目: 来源: 题型:
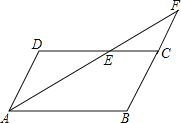
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=5,AD=3,AE平分∠DAB交BC的延长线于F点,则CF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.
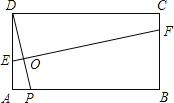
(1)当点E与点A重合时,折痕EF的长为 ;
(2)写出使四边形EPFD为菱形的x的取值范围,并求出当x=2时菱形的边长;
(3)令EF2=y,当点E在AD、点F在BC上时,写出y与x的函数关系式(写出x的取值范围).
相关试题

