【题目】如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.
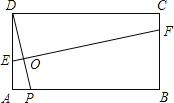
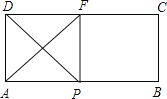
(1)当点E与点A重合时,折痕EF的长为 ;
(2)写出使四边形EPFD为菱形的x的取值范围,并求出当x=2时菱形的边长;
(3)令EF2=y,当点E在AD、点F在BC上时,写出y与x的函数关系式(写出x的取值范围).
参考答案:
【答案】(1)![]() ;(2)m=1.25,此时菱形EPFD的边长为1.25;(3)0≤x≤3﹣2
;(2)m=1.25,此时菱形EPFD的边长为1.25;(3)0≤x≤3﹣2![]() .
.
【解析】
试题分析:(1)当点E与点A重合时,得出∠DEF=∠FEP=45°,利用勾股定理得出答案即可;
(2)结合EF的长度得出x的取值范围,当x=2时,设PE=m,则AE=2﹣m,利用勾股定理得出答案;
(3)构造直角三角形,利用相似三角形的对应线段成比例确定y的值.
解:(1)∵纸片折叠,使点D与点P重合,得折痕EF,
当点E与点A重合时,
∵点D与点P重合是已知条件,
∴∠DEF=∠FEP=45°,
∴∠DFE=45°,即:ED=DF=1,
利用勾股定理得出EF=![]() ,
,
∴折痕EF的长为 ![]() .
.
故答案为:![]() ;
;
(2)∵要使四边形EPFD为菱形,
∴DE=EP=FP=DF,
只有点E与点A重合时,EF最长为![]() ,此时x=1,
,此时x=1,
当EF最长时,点P与B重合,此时x=3,
∴探索出1≤x≤3
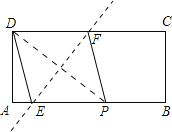
当x=2时,如图,连接DE、PF.
∵EF是折痕,
∴DE=PE,设PE=m,则AE=2﹣m
∵在△ADE中,∠DAP=90°,
∴AD2+AE2=DE2,即12+(2﹣m)2=m2,
解得 m=1.25,此时菱形EPFD的边长为1.25;
(3)过E作EH⊥BC;

∵∠EDO+∠DOE=90°,∠FEO+∠EOD=90°,
∴∠ODE=∠FEO,
∴△EFH∽△DPA,
∴![]() ,
,
∴FH=3x;
∴y=EF2=EH2+FH2=9+9x2;
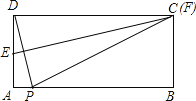
当F与点C重合时,如图,连接PF;
∵PF=DF=3,
∴PB=![]() ,
,
∴0≤x≤3﹣2![]() .
.
-
科目: 来源: 题型:
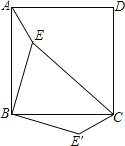
查看答案和解析>>【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C= 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 三角形的内心到三角形的三个顶点的距离相等 B. 三点确定一个圆
C. 垂直于半径的直线一定是这个圆的切线 D. 任何三角形有且只有一个内切圆
-
科目: 来源: 题型:
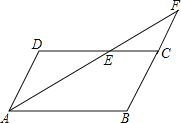
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=5,AD=3,AE平分∠DAB交BC的延长线于F点,则CF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AM是⊙O的直径,过点A作AP⊥AM.

(1)求证:∠PAC=∠ABC.
(2)连接PB与AC交于点D,与⊙O交于点E,F为BD上的一点,若M为BC的中点,且∠DCF=∠P,求证:
 =
=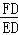 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径为4,线段OP=4,则点P与⊙O的位置关系是( )
A. 点P在⊙O外 B. 点P在⊙O内 C. 点P在⊙O上 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(-2,3)所在的象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
相关试题

