【题目】在平面直角坐标系xOy中,⊙C的半径为r(r>1),P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:若直线CP与⊙C交于点A,B,满足|PA-PB|=2,则称点P为⊙C的“完美点”,如图为⊙C及其“完美点”P的示意图.
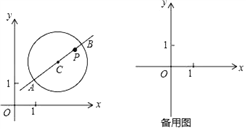
(1)当⊙O的半径为2时,
①点M(![]() ,0) ⊙O的“完美点”,点N(0,1) ⊙O的“完美点”,点T(-
,0) ⊙O的“完美点”,点N(0,1) ⊙O的“完美点”,点T(-![]() ,-
,- ![]() ) ⊙O的“完美点”(填“是”或者“不是”);
) ⊙O的“完美点”(填“是”或者“不是”);
②若⊙O的“完美点”P在直线y=![]() x上,求PO的长及点P的坐标;
x上,求PO的长及点P的坐标;
(2)⊙C的圆心在直线y=![]() x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
参考答案:
【答案】(1)①点M不是⊙O的“完美点”,点N是⊙O的“完美点”.点T是⊙O的“完美点”.
②OP=1,点P的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).(2)1
).(2)1![]() ≤t≤1+
≤t≤1+![]() .
.
【解析】解:(1)点M不是⊙O的“完美点”,
点N是⊙O的“完美点”.
点T是⊙O的“完美点”.
②根据题意,|PA![]() PB|=2,
PB|=2,
∴|OP+2![]() (2
(2![]() OP)|=2∴OP=1.
OP)|=2∴OP=1.
若点P在第一象限内,作PQ⊥x轴于点Q,∵点P在直线![]() 上,OP=1,
上,OP=1,
∴OQ=![]() ,PQ=
,PQ=![]() .∴P(
.∴P(![]() ,
, ![]() ).
).
若点P在第三象限内,根据对称性可知其坐标为(![]()
![]() ,
, ![]()
![]() ).
).
综上所述,PO的长为1,点P的坐标为(![]() ,
, ![]() )或(
)或(![]()
![]() ,
, ![]()
![]() ).
).
(2)对于⊙C的任意一个“完美点”P都有|PA﹣PB|=2,
∴|CP+2![]() (2
(2![]() CP)|=2.∴CP=1.
CP)|=2.∴CP=1.
∴对于任意的点P,满足CP=1,都有|CP+2![]() (2
(2![]() CP)|=2,
CP)|=2,
∴|PA﹣PB|=2,故此时点P为⊙C的“完美点”.因此,⊙C的“完美点”是以点C为圆心,1为半径的圆.
设直线![]() 与y轴交于点D,当⊙C移动到与y轴相切且切点在点D的下方时,t的值最小.
与y轴交于点D,当⊙C移动到与y轴相切且切点在点D的下方时,t的值最小.
设切点为E,连接CE,∵⊙C的圆心在直线y=![]() x+1上,∴此直线和x轴,y轴的交点C(0,1),F(﹣
x+1上,∴此直线和x轴,y轴的交点C(0,1),F(﹣![]() ,0),∴OF=
,0),∴OF=![]() ,OD=1,∵CE∥OF,∴△DOF∽△DEC,∴
,OD=1,∵CE∥OF,∴△DOF∽△DEC,∴![]() ,∴
,∴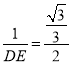 ,∴DE=
,∴DE=![]() .t的最小值为1
.t的最小值为1![]()
![]() .当⊙C移动到与y轴相切且切点在点D的上方时,t的值最大.
.当⊙C移动到与y轴相切且切点在点D的上方时,t的值最大.
同理可得t的最大值为1+![]() .综上所述,t的取值范围为1
.综上所述,t的取值范围为1![]()
![]() ≤t≤1+
≤t≤1+![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.

(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程3x=4x+5的解是( )
A.x=5
B.x=﹣3
C.x=﹣5
D.x=3 -
科目: 来源: 题型:
查看答案和解析>>【题目】贵州省是我国首个大数据综合试验区,大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值,为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:

(1)本次参与调查的人数有 人;
(2)关注城市医疗信息的有 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是 度;
(4)说一条你从统计图中获取的信息.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
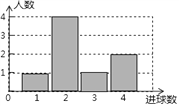
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个角60°的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2= .
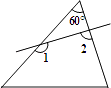
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数m,n,定义一种运算“※”:m※n=m2﹣mn﹣3.下列说法错误的是( )
A. 0※1=﹣3 B. 方程x※2=0的根为x1=﹣1,x2=3
C. 不等式组
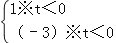 无解 D. 函数y=x※(﹣2)的顶点坐标是(1,﹣4)
无解 D. 函数y=x※(﹣2)的顶点坐标是(1,﹣4)
相关试题

