【题目】某自行车厂计划一周生产自行车2100辆,平均每天计制生产300辆,实际每天生产量与计划量相比有出入,下表是某周的生产情况.(超过每天计划生产数记为正,不足每天计划生产数记为负)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
每天超出计划的量数 |
|
|
|
|
|
|
|
(1)该厂星期四实际生产自行车______辆
(2)该厂本周实际每天平均生产多少辆自行车?
参考答案:
【答案】(1)313;(2)301.7.
【解析】
(1)根据题意和表格中提供的信息可以得到周四生产多少辆自行车;
(2)根据表格中的数据相加然后再加上标准乘以7,得到生产总量再除以7,即可解答本题.
(1)根据表格中的数据,可得周四生产的自行车为:300+13=313(辆).
故答案为:313
(2)[(+5)+(-2)+(-5)+(+13)+(-10)+(+14)+(-3)]+300×7
=12+2100
=2112(辆).
2112÷7≈301.7(辆).
即该厂本周实际每天平均生产301.7辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽量减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.假设商场降价
 元,
元,(1)降价
 元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含
元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含 的代数式表示);
的代数式表示);(2)若销售该童装每天盈利要达到1200元,则每件童装应该降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,点
中,点 是边
是边 上异于点
上异于点 的一点,
的一点, 的垂直平分线分别交
的垂直平分线分别交 、
、 于
于 ,连
,连 .
.(1)求证:
 ;
;(2)请求出:
 的度数;
的度数;(3)试猜想线段
 之间的数量关系并说明理由.
之间的数量关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b满足
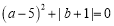 .请回管问题:
.请回管问题:(1)请直接写出a、b的值,a=______,b=_______.
(2)当x的取值范围是_________时,
 有最小值,这个最小值是_____.
有最小值,这个最小值是_____.(3)数轴a、b上两个数所对应的分别为A、B,AB的中点为点C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,当A、B两点重合时,运动停止.
①经过2秒后,求出点A与点B之间的距离AB.
②经过t秒后,请问:BC+AB的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,甲、乙、丙、丁、戊五名同学有以下说法:甲说:“直线BC不过点A”;乙说:“点A在直线CD外”; 丙说:“D在线段CB的反向延长线上;”丁说:“A,B,C,D两两连结,有5条线段” ; 戊说:“射线AD与射线CD不相交”. 其中说明正确的有( ).

A. 3人B. 4人C. 5人D. 2人
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
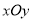 中,图形
中,图形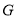 的投影矩形定义如下:矩形的两组对边分别平行于
的投影矩形定义如下:矩形的两组对边分别平行于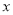 轴,
轴,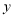 轴,图形
轴,图形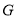 的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为
的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为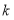 ,我们称常数
,我们称常数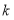 为图形
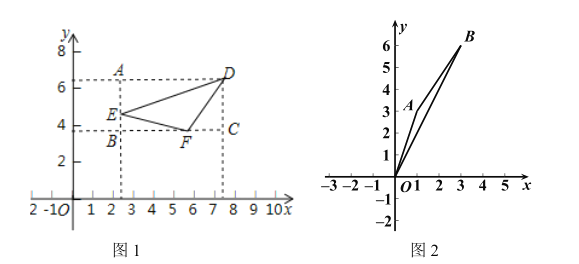
为图形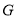 的投影比,如图1,矩形
的投影比,如图1,矩形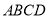 为
为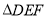 的投影矩形,其投影比
的投影矩形,其投影比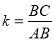 .
.
(1)如图2,若点
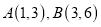 ,则
,则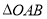 投影比
投影比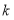 的值为________________;
的值为________________;(2)已知点
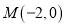 ,点
,点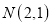 ,且
,且 投影比
投影比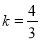 ,则
,则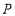 点坐标可能是__________(填写序号);
点坐标可能是__________(填写序号);①
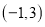 ②
② ③
③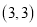 ④
④
(3)已知点
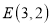 ,在直线
,在直线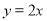 上有一点
上有一点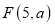 和一动点
和一动点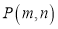 ,且
,且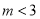 ,是否存在这样的
,是否存在这样的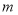 ,使得
,使得 的投影比
的投影比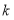 为定值?若存在,请求出
为定值?若存在,请求出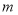 的范围及定值
的范围及定值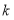 ;若不存在,请说明理由.
;若不存在,请说明理由.
相关试题

