【题目】如图,正方形![]() 中,点
中,点![]() 是边
是边![]() 上异于点
上异于点![]() 的一点,
的一点,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 、
、![]() 于
于![]() ,连
,连![]() .
.
(1)求证:![]() ;
;
(2)请求出:![]() 的度数;
的度数;
(3)试猜想线段![]() 之间的数量关系并说明理由.
之间的数量关系并说明理由.

参考答案:
【答案】(1)证明见解析 (2)90° (3)AE=DF+BM
【解析】
(1)本题考查垂直平分线的性质,按照其性质直接作答即可.
(2)本题考查全等三角形的判定,可通过做辅助线构造全等三角形,继而通过角度的等量替换解答本题.
(3)本题考查线段之间的数量关系,需要通过做辅助线构造全等三角形,利用全等性质推出边等,最后进行边的替换解答本题.
(1)∵EF是AM的垂直平分线
又∵点K在线段EF上
∴ KA=KM
(2)过K点作KQ,KT分别垂直于AB,BC,如下图所示
∵正方形ABCD,点K在其对角线BD上
∴KQ=KT,四边形QKTB为正方形
又∵KA=KM,∠KQA=∠KTM=90°
∴△KAQ![]() △KMT(HL)
△KMT(HL)
∴∠AKQ=∠TKM
∵∠QKT=90°
∴∠QKT=∠QKM+∠MKT=90°
∴∠QKT=∠QKM+∠AKQ=90°
∴∠AKM=90°

(3)过F点作FG⊥AB于G点,如下图所示
∴AG=DF,∠FEG+∠GFE=90°
∵EF⊥AM
∴∠BAM+∠FEG=90°
∴∠BAM=∠GFE
又∵∠FGE=∠ABM=90°,GF=AB
∴△FGE![]() △ABM(ASA)
△ABM(ASA)
∴GE=BM
故AE=AG+GE=DF+BM

-
科目: 来源: 题型:
查看答案和解析>>【题目】教材的
 课题学习
课题学习 要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠: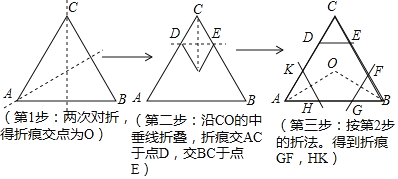
请你根据小明同学的折叠方法,回答以下问题:
 如果设正三角形ABC的边长为a,那么
如果设正三角形ABC的边长为a,那么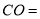 ______
______ 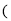 用含a的式子表示
用含a的式子表示 ;
;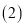 根据折叠性质可以知道
根据折叠性质可以知道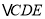 的形状为______ 三角形;
的形状为______ 三角形;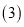 请同学们利用
请同学们利用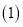 、
、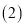 的结论,证明六边形KHGFED是一个六边形.
的结论,证明六边形KHGFED是一个六边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽量减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.假设商场降价
 元,
元,(1)降价
 元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含
元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含 的代数式表示);
的代数式表示);(2)若销售该童装每天盈利要达到1200元,则每件童装应该降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂计划一周生产自行车2100辆,平均每天计制生产300辆,实际每天生产量与计划量相比有出入,下表是某周的生产情况.(超过每天计划生产数记为正,不足每天计划生产数记为负)
星期
一
二
三
四
五
六
日
每天超出计划的量数
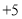
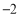
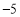
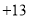
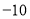
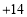
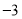
(1)该厂星期四实际生产自行车______辆
(2)该厂本周实际每天平均生产多少辆自行车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b满足
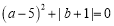 .请回管问题:
.请回管问题:(1)请直接写出a、b的值,a=______,b=_______.
(2)当x的取值范围是_________时,
 有最小值,这个最小值是_____.
有最小值,这个最小值是_____.(3)数轴a、b上两个数所对应的分别为A、B,AB的中点为点C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,当A、B两点重合时,运动停止.
①经过2秒后,求出点A与点B之间的距离AB.
②经过t秒后,请问:BC+AB的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,甲、乙、丙、丁、戊五名同学有以下说法:甲说:“直线BC不过点A”;乙说:“点A在直线CD外”; 丙说:“D在线段CB的反向延长线上;”丁说:“A,B,C,D两两连结,有5条线段” ; 戊说:“射线AD与射线CD不相交”. 其中说明正确的有( ).

A. 3人B. 4人C. 5人D. 2人
相关试题

