【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)由ASA即可得出结论;
(2)先证明四边形ABCD是平行四边形,再证明AD=AB,即可得出结论;
(3)由菱形的性质得出AC⊥BD,证明四边形ACED是平行四边形,得出AC=DE=2,AD=EC,由菱形的性质得出EC=CB=AB=2,得出EB=4,由勾股定理得BD═![]() ,即可得出答案.
,即可得出答案.
(1)∵点O是AC的中点,
∴AO=CO,
∵AM∥BN,
∴∠DAC=∠ACB,
在△AOD和△COB中,
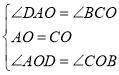 ,
,
∴△ADO≌△CBO(ASA);
(2)由(1)得△ADO≌△CBO,
∴AD=CB,
又∵AM∥BN,
∴四边形ABCD是平行四边形,
∵AM∥BN,
∴∠ADB=∠CBD,
∵BD平分∠ABN,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AD=AB,
∴平行四边形ABCD是菱形;
(3)由(2)得四边形ABCD是菱形,
∴AC⊥BD,AD=CB,
又DE⊥BD,
∴AC∥DE,
∵AM∥BN,
∴四边形ACED是平行四边形,
∴AC=DE=2,AD=EC,
∴EC=CB,
∵四边形ABCD是菱形,
∴EC=CB=AB=2,
∴EB=4,
在Rt△DEB中,由勾股定理得BD=![]() =
=![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
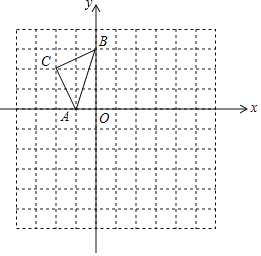
查看答案和解析>>【题目】如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).
(1)将△ABC绕原点O顺时针旋转90°得到△A1B1C1,画出△A1B1C1;
(2)以点O为位似中心,与△ABC位似的△A2B2C2满足A2B2:AB=2:1,请在网格内画出△A2B2C2,并直接填写△A2B2C2的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教材的
 课题学习
课题学习 要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠: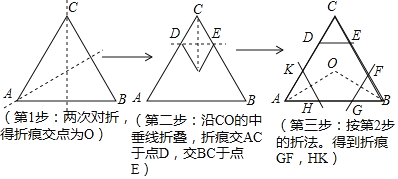
请你根据小明同学的折叠方法,回答以下问题:
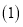 如果设正三角形ABC的边长为a,那么
如果设正三角形ABC的边长为a,那么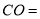 ______
______  用含a的式子表示
用含a的式子表示 ;
; 根据折叠性质可以知道
根据折叠性质可以知道 的形状为______ 三角形;
的形状为______ 三角形; 请同学们利用
请同学们利用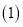 、
、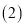 的结论,证明六边形KHGFED是一个六边形.
的结论,证明六边形KHGFED是一个六边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽量减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.假设商场降价
 元,
元,(1)降价
 元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含
元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含 的代数式表示);
的代数式表示);(2)若销售该童装每天盈利要达到1200元,则每件童装应该降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,点
中,点 是边
是边 上异于点
上异于点 的一点,
的一点, 的垂直平分线分别交
的垂直平分线分别交 、
、 于
于 ,连
,连 .
.(1)求证:
 ;
;(2)请求出:
 的度数;
的度数;(3)试猜想线段
 之间的数量关系并说明理由.
之间的数量关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂计划一周生产自行车2100辆,平均每天计制生产300辆,实际每天生产量与计划量相比有出入,下表是某周的生产情况.(超过每天计划生产数记为正,不足每天计划生产数记为负)
星期
一
二
三
四
五
六
日
每天超出计划的量数
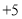
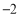
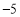
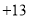
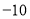
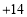
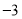
(1)该厂星期四实际生产自行车______辆
(2)该厂本周实际每天平均生产多少辆自行车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b满足
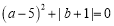 .请回管问题:
.请回管问题:(1)请直接写出a、b的值,a=______,b=_______.
(2)当x的取值范围是_________时,
 有最小值,这个最小值是_____.
有最小值,这个最小值是_____.(3)数轴a、b上两个数所对应的分别为A、B,AB的中点为点C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,当A、B两点重合时,运动停止.
①经过2秒后,求出点A与点B之间的距离AB.
②经过t秒后,请问:BC+AB的值是否随着时间t的变化而变化?若变化,请说明理由;若不变,请求其值.
相关试题

