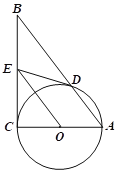
【题目】如图在RtΔABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
(1)求证:ED是⊙O的切线;
(2)如果⊙O的半径为1.5,ED=2,求AB的长.
(3)在(2)的条件下,求△ADO的面积.
参考答案:
【答案】(1)答案见解析;(2)5;(3)1.08.
【解析】
(1)连OD,首先证明△EOC≌△EOD,则可以证得∠EDO=∠ECO=90°,即可证得;
(2)证明OE是△ABC的中位线,在直角△OEC中,利用勾股定理求得OE的长,然后利用三角形中位线定理求得AB的长;
(3)连接CD,则CD是直角△ABC的斜边AB上的高,根据三角形的面积公式即可求得CD的长,则在直角△ACD中,利用勾股定理求得AD的长,则可求出△ACD的面积,进而求得△ADO的面积.
(1)连OD.
∵OE∥AB,∴∠EOC=∠A,∠EOD=∠ODA.
又∵OA=OD,∴∠A=∠ODA,∴∠EOC=∠EOD.
在△EOC和△EOD中,∵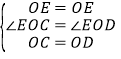 ,∴△EOC≌△EOD(SAS),∴∠EDO=∠ECO.
,∴△EOC≌△EOD(SAS),∴∠EDO=∠ECO.
又∵∠ECO=90°,∴∠EDO=90°即ED⊥DO 而点D在⊙O上,∴ED为⊙O的切线.
(2)∵OE∥AB,OA=OC,∴AB=2OE.
在△OCE中,OE=![]()
![]() ,∴AB=2OE=5;
,∴AB=2OE=5;
(3)连结CD.
∵AC=2OA=3,AB=5,∴BC=![]() =
=![]() =4.
=4.
∵AC是⊙O的直径,∴∠CDA=90°,∴CD⊥AB.
在Rt△ABC中,CD⊥AB,∴CDAB=ACBC,∴CD=2.4.
在Rt△ACD中,AD=![]() =
=![]() =1.8,∴S△ACD=
=1.8,∴S△ACD=![]() CDAD=2.16,∴S△ADO=
CDAD=2.16,∴S△ADO=![]() S△ACD=1.08.
S△ACD=1.08.
-
科目: 来源: 题型:
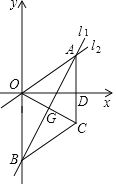
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y
 x与直线l:y=kx+b相交于点A(a,3),直线交l交y轴于点B(0,﹣5).
x与直线l:y=kx+b相交于点A(a,3),直线交l交y轴于点B(0,﹣5).(1)求直线l的解析式;
(2)将△OAB沿直线l翻折得到△CAB(其中点O的对应点为点C),求证:AC∥OB;
(3)在直线BC下方以BC为边作等腰直角三角形BCP,直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三条线段的长分别为
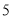 厘米,
厘米, 厘米,
厘米,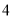 厘米,以其中两条为对角线,另一条为一边,可以画出______个平行四边形.
厘米,以其中两条为对角线,另一条为一边,可以画出______个平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2 - 2(1-m)x+m2的两实数根为x1,x2.
(1)求m的取值范围;
(2)设
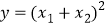 ,当m为何值时,y有最小值,求y的最小值.
,当m为何值时,y有最小值,求y的最小值. -
科目: 来源: 题型:
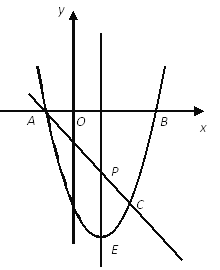
查看答案和解析>>【题目】如图,抛物线
 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
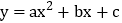 (a≠0)的图象如图所示,则下列结论中正确的是
(a≠0)的图象如图所示,则下列结论中正确的是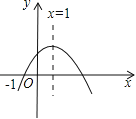
A. a>0 B. 当﹣1<x<3时,y>0
C. c<0 D. 当x≥1时,y随x的增大而增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数
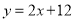 的图像分别交
的图像分别交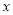 轴、
轴、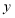 轴于
轴于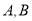 两点.过点
两点.过点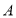 的直线交
的直线交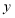 轴正半轴于点
轴正半轴于点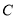 ,且点
,且点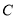 为线段
为线段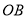 的中点.
的中点.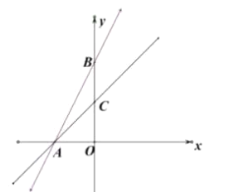
(1)求直线
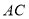 的表达式;
的表达式;(2)如果四边形
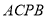 是平行四边形,求点
是平行四边形,求点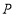 的坐标.
的坐标.
相关试题

