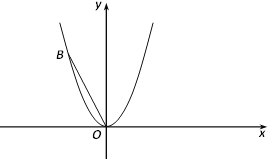
【题目】如图,平面直角坐标系xOy中,抛物线![]() 经过点B(-2,4).
经过点B(-2,4).
(1)求a的值;
(2)作Rt△OAB,使∠BOA=90°,且OB=2OA,求点A坐标;
(3)在(2)的条件下,过点A作直线AC⊥x轴于点C,交抛物线![]() 于点D,将该抛物线向左或向右平移t(t>0)个单位长度,记平移后点D的对应点为D′,点B的对应点为B′.当CD′+OB′的值最小时,请直接写出t的值和平移后相应的抛物线解析式.
于点D,将该抛物线向左或向右平移t(t>0)个单位长度,记平移后点D的对应点为D′,点B的对应点为B′.当CD′+OB′的值最小时,请直接写出t的值和平移后相应的抛物线解析式.
参考答案:
【答案】(1) ![]() .(2) (2,1)或(-2,-1).(3) t=1,
.(2) (2,1)或(-2,-1).(3) t=1, ![]() .
.
【解析】分析:(1)直接利用待定系数法求出抛物线解析式即可;(2)分两种情况讨论:点A在第一象限;点A在第三象限;(3)过点O作![]() 的平行线,再作点
的平行线,再作点![]() 关于x轴的对称点,利用勾股定理即可求解.
关于x轴的对称点,利用勾股定理即可求解.
(1)将点B(-2,4)代入y=ax (a≠0)得4a=4,∴a=1.
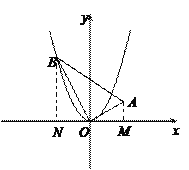
(2)如图①,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,
∴∠OMA=∠BNO=90°,∴∠NBO+∠NOB=90°.
∵∠BOA=90°,∴∠NOB+∠MOA=90°,
∴∠NBO=∠MOA,∴△BNO∽△OMA,
∴![]() .∵BN=4,NO=2,
.∵BN=4,NO=2,
∴OM=2,MA=1,
∴A点坐标为(2,1).
如图②,过点A作AM⊥y轴于点M,过点B作BN⊥y轴于点N,
同上可得OM=1,MA=2,
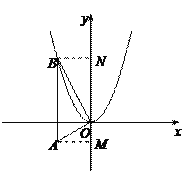
∴A点坐标为(-2,-1).
综上所述,A点坐标为(2,1)或(-2,-1).
(3)t=1, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2x2向左平移3个单位,再向上平移1个单位得到的抛物线,其解析式是( )
A.y=2(x+3)2+1B.y=2(x﹣3)2﹣1
C.y=2(x+3)2﹣1D.y=2(x﹣3)2+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】用半径为2cm的半圆围成一个圆锥的侧面,这个圆锥的底面半径为( )
A.1cm
B.2cm
C.πcm
D.2πcm -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D在AB边上,AD=CD,DE⊥AC于点E,CF∥AB,交DE的延长线于点F.
(1)如图1,求证:四边形ADCF是菱形;
(2)如图2,当∠ACB=90°,∠B=30°时,在不添加辅助线的情况下,请直接写出图中与线段AC相等的线段(线段AC除外).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红做一道数学题“两个多项式A,B,B为
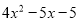 ,试求A+2B的值”.小红误看成A-2B,结果答案(计算正确)为
,试求A+2B的值”.小红误看成A-2B,结果答案(计算正确)为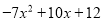 .
.(1)你能求出多项式A吗?
(2)试求A+2B的正确结果;
(3)求出当
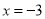 时A+2B的值.
时A+2B的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:(m+1)(m﹣9)+8m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:

(1)根据上面多面体的模型,完成表格中的空格:
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
12
正八面体
8
12
正十二面体
20
12
30
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是E=________;
(3)一个多面体的面数比顶点数大8,棱数为30,则这个多面体的面数是多少?
相关试题

