【题目】在△ABC中,点D在AB边上,AD=CD,DE⊥AC于点E,CF∥AB,交DE的延长线于点F.
(1)如图1,求证:四边形ADCF是菱形; 
(2)如图2,当∠ACB=90°,∠B=30°时,在不添加辅助线的情况下,请直接写出图中与线段AC相等的线段(线段AC除外). 
参考答案:
【答案】
(1)证明:如图1,
∵AD=CD,DE⊥AC,
∴∠DCA=∠ADC,CE=AE,
∵CF∥AB,
∴∠ECF=∠EAD,
∴∠DCA=∠ECF,
即CE平分∠DCF,
而CE⊥DF,
∴CD=CF,
∴AD∥CF,
∴四边形ADCF为平行四边形,
而DA=DC,
∴四边形ADCF是菱形

(2)解:如图2,∵∠ACB=90°,∠B=30°,
∴∠BAC=60°,
而DA=DC,
∴△ADC为等边三角形,
∴AC=AD=CD,∠ACD=60°,
∵四边形ADCF为菱形,
∴AC=AD=DC=CF=AF,
∵∠B=∠DCB=30°,
∴BD=CD,
∴AC=AD=DC=CF=AF=BD

【解析】(1)如图1,利用等腰三角形的性质得∠DCA=∠ADC,CE=AE,再利用CF∥AB得到∠ECF=∠EAD,则∠DCA=∠ECF,于是根据等腰三角形的判定方法可得CD=CF,所以四边形ADCF为平行四边形,
加上DA=DC可判断四边形ADCF是菱形;(2)如图2,先证明△ADC为等边三角形得到AC=AD=CD,∠ACD=60°,再利用菱形的性质可得AC=AD=DC=CF=AF,然后证明BD=CD即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A.(a+1)2=a2+1
B.a2+a3=a5
C.a8÷a2=a6
D.3a2﹣2a2=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2x2向左平移3个单位,再向上平移1个单位得到的抛物线,其解析式是( )
A.y=2(x+3)2+1B.y=2(x﹣3)2﹣1
C.y=2(x+3)2﹣1D.y=2(x﹣3)2+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】用半径为2cm的半圆围成一个圆锥的侧面,这个圆锥的底面半径为( )
A.1cm
B.2cm
C.πcm
D.2πcm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系xOy中,抛物线
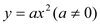 经过点B(-2,4).
经过点B(-2,4).(1)求a的值;
(2)作Rt△OAB,使∠BOA=90°,且OB=2OA,求点A坐标;
(3)在(2)的条件下,过点A作直线AC⊥x轴于点C,交抛物线
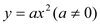 于点D,将该抛物线向左或向右平移t(t>0)个单位长度,记平移后点D的对应点为D′,点B的对应点为B′.当CD′+OB′的值最小时,请直接写出t的值和平移后相应的抛物线解析式.
于点D,将该抛物线向左或向右平移t(t>0)个单位长度,记平移后点D的对应点为D′,点B的对应点为B′.当CD′+OB′的值最小时,请直接写出t的值和平移后相应的抛物线解析式.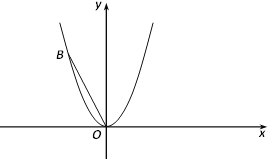
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红做一道数学题“两个多项式A,B,B为
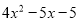 ,试求A+2B的值”.小红误看成A-2B,结果答案(计算正确)为
,试求A+2B的值”.小红误看成A-2B,结果答案(计算正确)为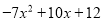 .
.(1)你能求出多项式A吗?
(2)试求A+2B的正确结果;
(3)求出当
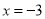 时A+2B的值.
时A+2B的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:(m+1)(m﹣9)+8m= .
相关试题

