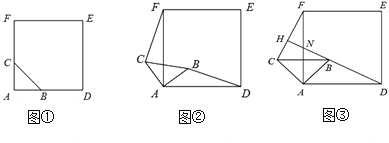
【题目】如图①,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转![]()
![]() 时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由;
时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H;
(ⅰ)求证:BD⊥CF;
(ⅱ)当AB=2,AD=![]() 时,求线段DH的长.
时,求线段DH的长.
参考答案:
【答案】(1)详见解析;(2)①详见解析;②![]() .
.
【解析】试题分析:(1)根据旋转变换的性质和全等三角形的判定定理证明
![]() ≌
≌![]() 证明结论;
证明结论;
(2)①根据全等三角形的性质、垂直的定义证明即可;
②连接DF,延长AB交DF于M,根据题意和等腰直角三角形的性质求出DM、BM的长,根据勾股定理求出BD的长,根据相似三角形的性质列出比例式,计算即可得到答案.
试题解析:(1)BD=CF.
理由如下:由题意得,∠CAF=∠BAD= ![]() ,
,
在△CAF和△BAD中,
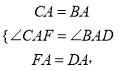 ∴△CAF≌△BAD,
∴△CAF≌△BAD,
∴BD=CF;
(2)①由(1)得△CAF≌△BAD,
∴∠CFA=∠BDA,
![]()
![]()
![]() ,即BD⊥CF;
,即BD⊥CF;
②连接DF,延长AB交DF于M,
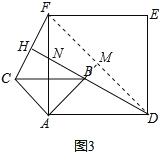
∵四边形ADEF是正方形, ![]()
∴AM=DM=3,BM=AMAB=1,
∵△ABC绕点A逆时针旋转![]() ,
,
∴∠BAD=![]() ,
,
∴AM⊥DF,
![]()
![]()
![]() 又
又![]()
∴△DMB∽△DHF,
![]() 即
即![]()
解得, ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学八年级组织了一次“汉字听写比赛”,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,语文教研组将八年级一班和二班的成绩整理并绘制成如下的统计图,请根损换供的信息解答下列问题.
(1)把一班比赛成统计图补充完整;

(2)填表:
平均数(分)
中位数(分)
众数(分)
一班
a
b
85
二班
84
75
c
表格中:a=______,b=______,c=_______.
(3)请从以下给出的两个方面对这次比赛成绩的结果进行分析:
①从平均数、众数方面来比较一班和二班的成绩;
②从B级以上(包括B级)的人数方面来比较-班和二班的成绩.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(4,n),B(2,4)是一次函数y=kx+b的图象和反比例函数
 的图象的两个交点;
的图象的两个交点;
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式kx+b
 <0的解集(请直接写出答案).
<0的解集(请直接写出答案). -
科目: 来源: 题型:
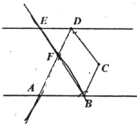
查看答案和解析>>【题目】如图,已知
 为两条相互平行的直线
为两条相互平行的直线 ,
, 之间一点,
之间一点, 和
和 的角平分线相交于
的角平分线相交于 ,
, .
. 

(1)求证:
 ;
;(2)连结
 当
当 且
且 时,求
时,求 的度数;
的度数; (3)若
 时,将线段
时,将线段 沿直线
沿直线  方向平移,记平移后的线段为
方向平移,记平移后的线段为 (
( ,
, 分别对应
分别对应 、
、 当
当 时,请直接写出
时,请直接写出 的度数_______.
的度数_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形ABCD中,
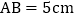 ,
, ,点P从A开始沿边AB向终点B以
,点P从A开始沿边AB向终点B以 的速度移动,与此同时,点Q从点B开始沿边BC向终点C以
的速度移动,与此同时,点Q从点B开始沿边BC向终点C以 的速度移动,如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动
的速度移动,如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动 设运动时间为t秒.
设运动时间为t秒. 填空:
填空: ________,
________, ________
________ 用含t的代数式表示
用含t的代数式表示 :
: 当t为何值时,PQ的长度等于5cm?
当t为何值时,PQ的长度等于5cm? 是否存在t的值,使得五边形APQCD的面积等于
是否存在t的值,使得五边形APQCD的面积等于 ?若存在,请求出此时t的值;若不存在,请说明理由.
?若存在,请求出此时t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
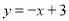 与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线
与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线 与x轴的另一个交点为A,顶点为P.
与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分14分)如图,在正方形ABCD中,AB=5.点E为BC边上一点(不与点B重合),点F为CD边上一点,线段AE、BF相交于点O,其中AE=BF.

(1)求证:AE⊥BF;
(2)若OA-OB=1,求OA的长及四边形OECF的面积;
(3)连接OD,若△AOD是以AD为腰的等腰三角形,求AE的长.
相关试题

