搜索
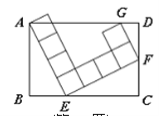
【题目】如图，矩形ABCD中，由8个面积均为1的小正方形组成的L型模板如图放置，则矩形ABCD的周长为 _ ．
参考答案：
【答案】
．
【解析】
试题分析：根据AAS可以证明△ABE≌△ECF，得AB=CE，BE=CF；根据两角对应相等，可以证明△ECF∽△FDG，则DF：CE=FG：EF=1：2．设BE=x，则AB=2x，根据勾股定理求得x的值，进而求得矩形的面积．
根据等角的余角相等，得
∠BAE=∠CEF=∠DFG．
又∠B=∠C=∠D=90°，AE=EF=4，FG=2，
∴△ABE≌△ECF，△ECF∽△FDG．
∴AB=CE，BE=CF，DF：CE=FG：EF=1：2．
设BE=x，则AB=2x，根据勾股定理，得
x2+4x2=16，
x=
．
则矩形ABCD的面积为：2x×3x=6x2=．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图, ⊙O 的半径是2，直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点，且在直线l的异侧,若∠AMB＝45°,则四边形MANB 面积的最大值是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在等腰Rt△ABC中，∠BAC=90°，点E在AC上（且不与点A、C重合），在△ABC的外部作等腰Rt△CED，使∠CED=90°，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．
（1）请直接写出线段AF，AE的数量关系；
（2）①将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；
②若AB=2
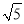，CE=2，在图②的基础上将△CED绕点C继续逆时针旋转一周的过程中，当平行四边形ABFD为菱形时，直接写出线段AE的长度．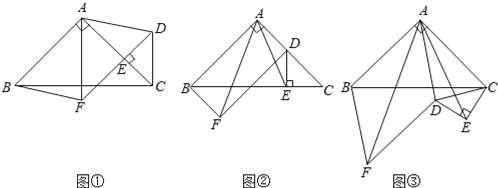
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c与x轴交于点A（-2，0），顶点坐标为（2，n），与y轴的交点在（0，3），（0，4）之间（包含端点），则下列结论：①当x＞6时，y＜0；②5a+b＞0；③
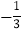≤a≤-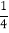
，④4≤n＜5中，正确有（ ）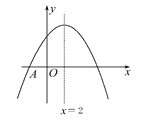
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】有四个三角形，分别满足下列条件：（1）一个角等于另外两个内角之和；（2）三个内角之比为3：4：5；（3）三边之比为5：12：13；（4）三边长分别为5，24，25．其中直角三角形有（ ）
A. 1个B. 2个C. 3个D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列三个结论：
①∠BOC=90°+
∠A；②设OD＝m，AE＋AF＝n，则S△AEF＝mn；③EF是△ABC的中位线．其中正确的结论是________．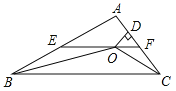
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，已知AB=5，BC=8，AC=7，动点P、Q分别在边AB、AC上，使△APQ的外接圆与BC相切，则线段PQ的最小值等于_______________．
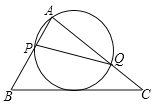
相关试题
