【题目】有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上上生出两个小正方形(如图1),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2017次后形成的图形中所有正方形的面积和是( )
A.2015
B.2016
C.2017
D.2018
参考答案:
【答案】D
【解析】解:设直角三角形的是三条边分别是a,b,c.
根据勾股定理,得a2+b2=c2 ,
即正方形A的面积+正方形B的面积=正方形C的面积=1.
推而广之,“生长”了2017次后形成的图形中所有的正方形的面积和是2018×1=2018.
故选D.
【考点精析】关于本题考查的勾股定理的概念,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )
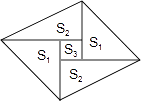
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2-3x+a2-1经过坐标原点,且开口向下,则实数a的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件为必然事件的是( )
A.打开电视机,播放频道正好是山西电视台
B.从一副扑克牌中任意抽出一张牌,花色是黑桃
C.买一张电影票,座位号正好是奇数
D.口袋中装有4个红球和2个白球,从中摸出3个球,其中必有红球
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:S1=1+
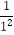 +
+ 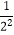 ,S2=1+
,S2=1+ 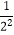 +
+ 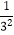 ,S3=1+
,S3=1+ 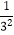 +
+ 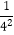 ,S4=1+
,S4=1+ 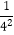 +
+ 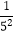 ,S5=1+
,S5=1+ 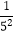 +
+ 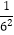 ,…则
,…则 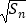 =(用含n的代数式表示,其中n为正整数)
=(用含n的代数式表示,其中n为正整数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c满足|a﹣
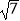 |+
|+  +(c﹣4
+(c﹣4 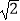 )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从热气球C处测得地面A、B两点的俯角分别为45°、30°,如果此时热气球C处离地面的高度CD为100米,且点A、D、B在同一直线上,求AB两点间的距离(结果保留根号)

相关试题

