【题目】如图所示,在每个边长都为1的小正方形组成的网格中,点A,B,C均为格点.
(Ⅰ)线段AB的长度等于 ![]()
(Ⅱ)若P为线段AB上的动点,以PC、PA为邻边的四边形PAQC为平行四边形,当PQ长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法(不要求证明).
参考答案:
【答案】解:(Ⅰ)线段AB的长度为: ![]() =5;(Ⅱ)如图所示:四边形PAQC即为所求.
=5;(Ⅱ)如图所示:四边形PAQC即为所求.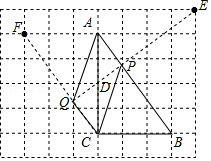
故答案为:5.
【解析】(Ⅰ)根据勾股定理可求线段AB的长度;(Ⅱ)取格点D,E,F,连结DE与AB交于点P,延长ED与CF交于点,四边形PAQC即为所求.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
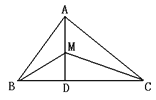
A. 9 B. 35 C. 45 D. 无法计算
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(Ⅰ)直接写出点B坐标 ;判断△OBP的形状
;判断△OBP的形状  ;
;
(Ⅱ)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD=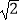 S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.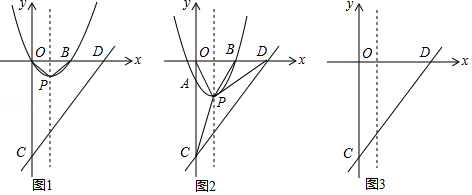
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )

A.∠ECD=112.5°
B.DE平分∠FDC
C.∠DEC=30°
D.AB= CD
CD -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程(1)
 =2;(2)5x﹣2=2x﹣(3﹣2x);(3)xy=5;(4)
=2;(2)5x﹣2=2x﹣(3﹣2x);(3)xy=5;(4)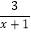 =﹣2;(5)x2﹣x=1;(6)x=0中一元一次方程有( )
=﹣2;(5)x2﹣x=1;(6)x=0中一元一次方程有( )A. 2个 B. 3个 C. 4个 D. 5个
相关试题

