【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

参考答案:
【答案】(1)证明过程见解析;(2)8.
【解析】试题分析:(1)由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;(2)由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.
试题解析:(1)∵四边形ABCD是平行四边形, ∴AD∥BC,AB∥CD,
∴∠DAE=∠F,∠D=∠ECF, ∵E是ABCD的边CD的中点, ∴DE=CE,
在△ADE和△FCE中,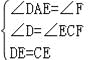 ,∴△ADE≌△FCE(AAS);
,∴△ADE≌△FCE(AAS);
(2)∵ADE≌△FCE, ∴AE=EF=3, ∵AB∥CD, ∴∠AED=∠BAF=90°,
在ABCD中,AD=BC=5, ∴DE=![]() =
=![]() =4, ∴CD=2DE=8
=4, ∴CD=2DE=8
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的周长为18,一边长x由小到大变化,则长方形的面积y与这个边长x的关系式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD或BD的延长线,垂足为E,如图.

(1)若BD是AC的中线,求 的值;
的值;
(2)若BD是∠ABC的角平分线,求 的值;
的值;
(3)结合(1)、(2),试推断 的取值范围(直接写出结论,不必证明),并探究
的取值范围(直接写出结论,不必证明),并探究  的值能小于
的值能小于  吗?若能,求出满足条件的D点的位置;若不能,说明理由.
吗?若能,求出满足条件的D点的位置;若不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的伴随方程,这个根在数轴上对应的点该不等式组的伴随点.
(1)在方程①
 ,②
,② ,③
,③ 中,不等式组
中,不等式组 的伴随方程是 ;(填序号)
的伴随方程是 ;(填序号)(2)如图,M、N都是关于
 的不等式组
的不等式组 的伴随点,求
的伴随点,求 的取值范围.
的取值范围.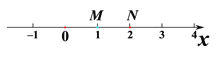
(3)不等式组
 的伴随方程的根有且只有2个整数,求
的伴随方程的根有且只有2个整数,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2+1)(22+1)(24+1)(28+1)(216+1)
相关试题

