【题目】如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( ) 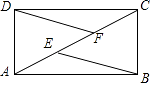
A.![]()
B.1
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:∵矩形ABCD中,AB=4,AD=2, ∴AB∥CD,AB=CD,∠BAD=∠ABC=90°,矩形ABCD的面积=4×2=8,
∴∠DCF=∠BAE,
在△DCF和△BAE中, 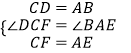 ,
,
∴△DCF≌△BAE(SAS),
∴DF=BE,∠DFC=∠BEA,
∴∠DFE=∠BEF,
∴DF∥BE,
∵AE=EF=FC,
∴△BCE的面积= ![]() ×8=
×8= ![]() ,
,
延长BE交AD于G,延长DF交BC于H,作FM⊥BE于M,CN⊥BE于N,则FM∥CN,
∵AE=EF=FC,
∴AG=DG=1,BH=CH=1,
∴BG= ![]() =
= ![]() ,
,
∴BE= ![]() BG=
BG= ![]() ,
,
∵ ![]() BECN=
BECN= ![]() ,
,
∴CN= ![]() ,
,
∵FM∥CN,EF=FC,
∴FM= ![]() CN=
CN= ![]() ,
,
故选:D.
【考点精析】关于本题考查的矩形的性质,需要了解矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )

A.5cm
B.10cm
C.20cm
D.15cm -
科目: 来源: 题型:
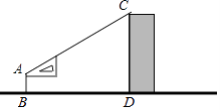
查看答案和解析>>【题目】如图是小华利用含30°角的三角板测量楼房高度的示意图,已知桌子高AB为1米,地面上B和D之间的距离为100米,则楼高CD约为( )
A.51米
B.59米
C.88米
D.174米 -
科目: 来源: 题型:
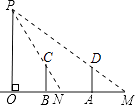
查看答案和解析>>【题目】如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( )
A.变长了1.5米
B.变短了2.5米
C.变长了3.5米
D.变短了3.5米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形ABCD,也可以拼成正方形EFGH,则菱形ABCD面积和正方形EFGH面积之比为( )

A.1
B.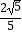
C.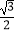
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的
 时,求出这时点M的坐标.
时,求出这时点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:①PA=PB+PC;②
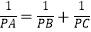 ;③PAPE=PBPC.其中,正确结论的个数为( )
;③PAPE=PBPC.其中,正确结论的个数为( ) 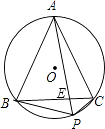
A.3个
B.2个
C.1个
D.0个
相关试题

